Motivation
In many practical cases the reservoir flow created by well or group of wells is getting aligned with a specific linear direction away from wells (see linear fluid flow).
This happens when wells are placed in a channel or a narrow compartment.
It also happens around fracture planes and conductive faults. It also develops temporarily at early times of the transients in horizontal wells.
This type of flow is called linear fluid flow and corresponding PTA type library models provides a reference for linear fluid flow diagnostics.
Inputs & Outputs
| Inputs | Outputs | ||
|---|---|---|---|
q_t | total sandface rate | p(t,x) | reservoir pressure |
p_i | initial formation pressure | p_{wf}(t) | well bottomhole pressure |
d | reservoir channel width | ||
\sigma | transmissibility,
\sigma = \frac{k \, h}{\mu} | ||
\chi | pressure diffusivity,
\chi = \frac{k}{\mu} \, \frac{1}{\phi \, c_t} | ||
Physical Model
| Linear fluid flow | Homogenous reservoir | Infinite boundary | Zero wellbore radius | Slightly compressible fluid flow | Constant rate production |
|---|---|---|---|---|---|
p(t, {\bf r}) \rightarrow p(t, x) {\bf r} \in ℝ^2 = \{ x, y\} | M(x, p)=M =\rm const \phi(x, p)=\phi =\rm const h(x)=h =\rm const | 0 \leq x \rightarrow \infty | x_w = 0 | c_t(p) = c_r +c = \rm const | q_t = \rm const |
Mathematical Model
Applications
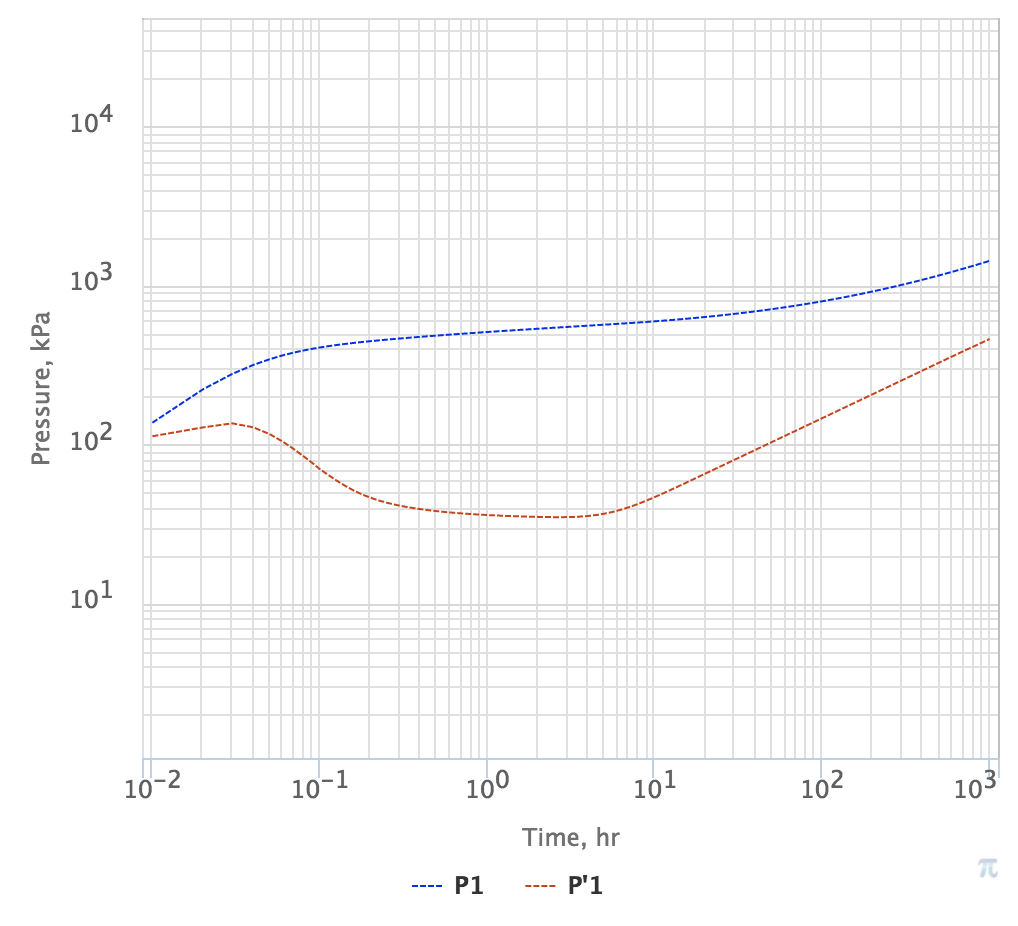
Pressure Testing – Channel or Narrow reservoir compartment
Pressure Drop |
| |||
Log derivative |
| |||
| Fig. 2. PTA Diagnostic plot for linear fluid flow in reservoir channel |
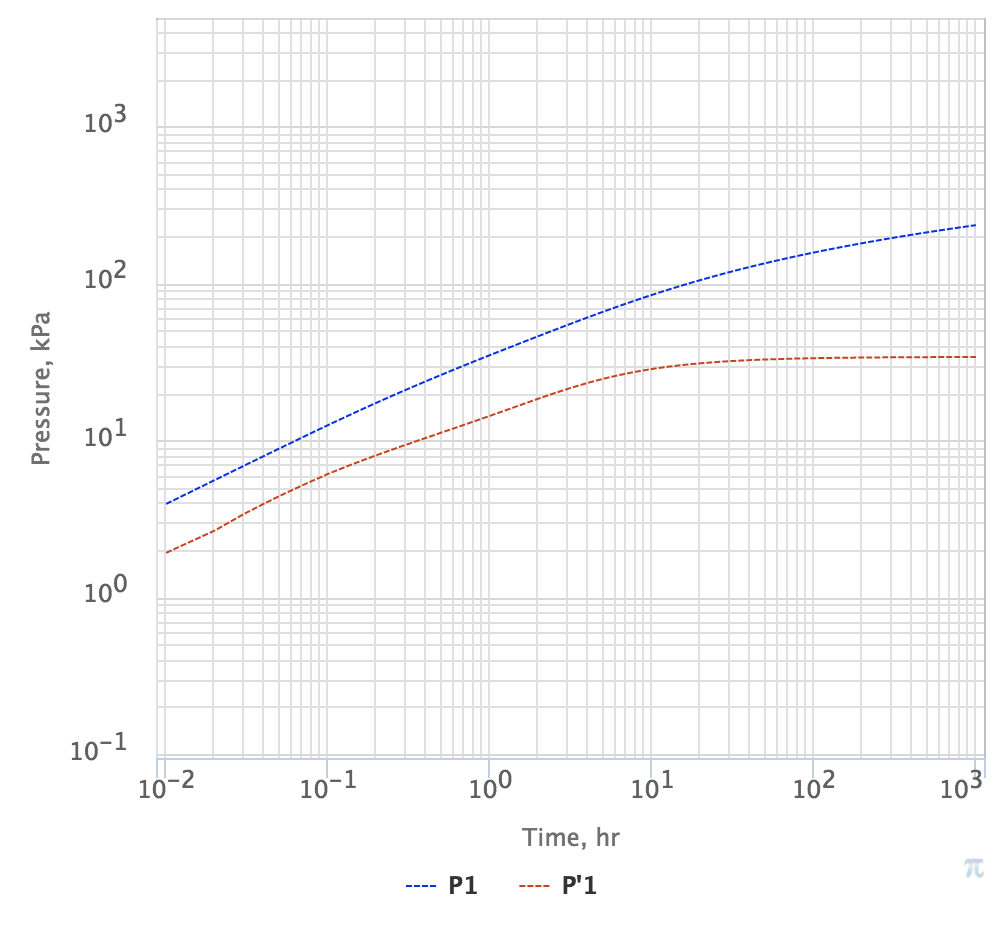
Pressure Testing – Infinite conductivity fracture
Pressure Drop |
| |||
Log derivative |
| |||
| Fig. 2. PTA Diagnostic plot for linear fluid flow in infinite conductivity fracture |
See also
Physics / Fluid Dynamics / Linear fluid flow
[ Radial Flow Pressure @model ] [ 1DR pressure diffusion of low-compressibility fluid ] [ Exponential Integral ]
[ Petroleum Industry / Upstream / Subsurface E&P Disciplines / Well Testing / Pressure Testing ]