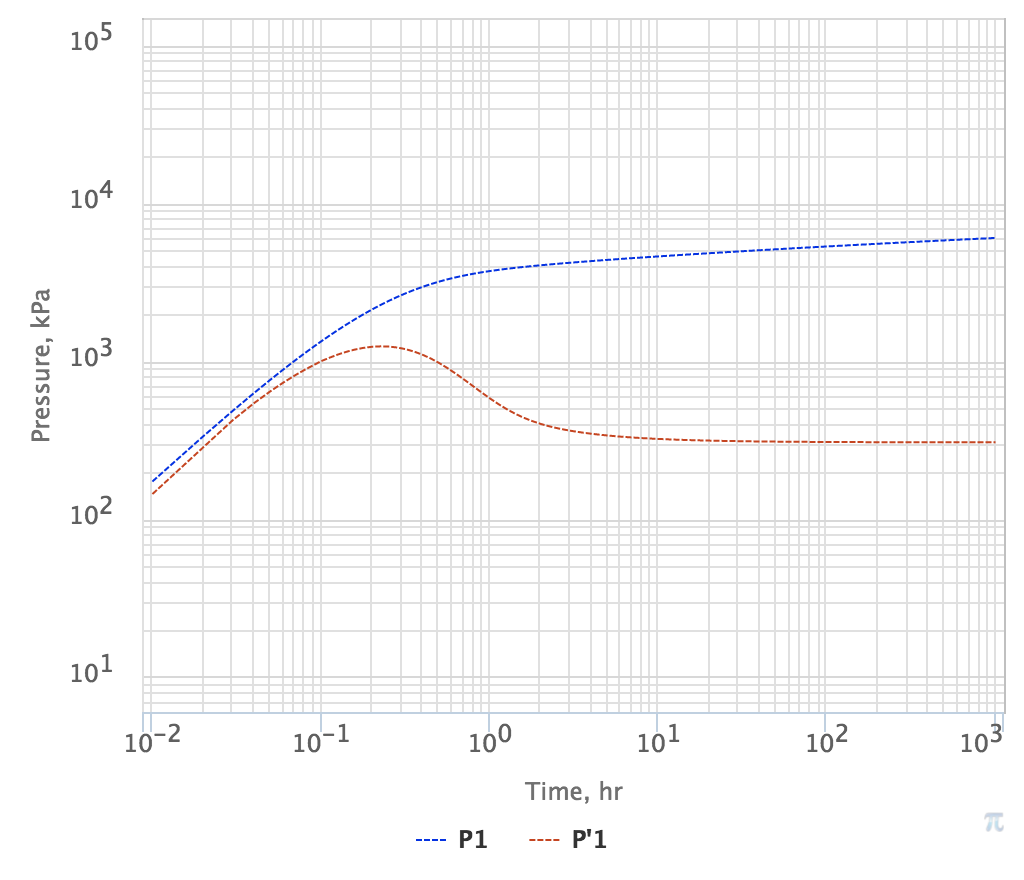
Motivation
In many practical cases the reservoir fluid flow created by well is getting aligned with a radial direction towards or away from well.
This type of reservoir fluid flow is called radial fluid flow and corresponding pressure diffusion models provide a diagnostic basis for pressure-rate base reservoir flow analysis.
The radial flow can be infinite acting or boundary dominated or transiting from one to another.
Although the actual reservoir fluid flow may not have an axial symmetry around the well-reservoir contact or around reservoir inhomogeneities (like boundary and faults and composite areas) but still in many practical cases the reservoir flow tends to become radial after some time which makes a Radial Flow Pressure Diffusion @model (in its general form or in particular BVP solution) a popular diagnostic tool.
Physical Model
Mathematical Model
| Expand |
|---|
|
| LaTeX Math Block |
|---|
| r_{wf} < r \leq r_e |
|
| LaTeX Math Block |
|---|
| \frac{\partial p}{\partial t} = \chi \, \left( \frac{\partial^2 p}{\partial r^2} + \frac{1}{r} \frac{\partial p}{\partial r} \right) |
|
| LaTeX Math Block |
|---|
| p(t = 0, {\bf r}) = p_i |
|
| LaTeX Math Block |
|---|
| p(t, r \rightarrow r_e ) = p_i) |
or | LaTeX Math Block |
|---|
| \left[ \frac{\partial p}{\partial r} \right]_{r =r_e} = 0 |
|
| LaTeX Math Block |
|---|
| \left[ r\frac{\partial p(t, r )}{\partial r} \right]_{r \rightarrow r_w} = \frac{q_t}{2 \pi \sigma} |
|
| LaTeX Math Block |
|---|
| p_{wf}(t)= p(t,r_w) - S \cdot r_w \, \frac{\partial p}{\partial r} \Bigg|_{r=r_w} |
|
|
| Expand |
|---|
|
There is no universal analytical solution to the above problem | LaTeX Math Block Reference |
|---|
|
–| LaTeX Math Block Reference |
|---|
|
but it can be always presented as below:
| LaTeX Math Block |
|---|
| p(t,r) = p_i - \frac{q_t}{4 \pi \sigma} \, F \bigg( - \frac{r^2}{4 \chi t} \bigg) |
|
| LaTeX Math Block |
|---|
| p_{wf}(t) = p_i - \frac{q_t}{4 \pi \sigma} \, \bigg[2S + F \bigg( - \frac{r_w^2}{4 \chi t} \bigg) \bigg] |
|
where a single-argument function describing the peculiarities of the diffusion model (well geometry, penetration geometry, formation inhomogeneities, hydraulic fractures, boundary conditions, etc.).The fact that solution of equations | LaTeX Math Block Reference |
|---|
|
–| LaTeX Math Block Reference |
|---|
|
can be presented as | LaTeX Math Block Reference |
|---|
|
–| LaTeX Math Block Reference |
|---|
|
finds a lot of practical applications in Well Testing.
|
Applications
Equations
| LaTeX Math Block Reference |
|---|
|
and
| LaTeX Math Block Reference |
|---|
|
show how the
basic diffusion model parameters impact the pressure response while other diffusion parameters are encoded in
function and play important methodological role as they are used in many algorithms and express-methods of
Pressure Testing.
| Expand |
|---|
| title | Line Source Solution |
|---|
|
In case of infinite homogeneous reservoir, produced by a infinitely small vertical well with no skin and no wellbore storage the function has an exact analytical formula, given by exponential integral | LaTeX Math Inline |
|---|
| body | F(z) = - {\rm Ei} (z) |
|---|
|
(see Line Source Solution (LSS) @model).
|
| Expand |
|---|
|
Isobar equation for a constant-rate production: | LaTeX Math Block |
|---|
| p(t,r) = p_i + \frac{q_t}{4 \pi \sigma} \, F \bigg( - \frac{r^2}{4 \chi t} \bigg) = {\rm const} \quad \rightarrow \quad \frac{r^2}{4 \chi t}= {\rm const} |
Since the pressure disturbance at
moment was at well walls then the formula for constant-pressure front propagation becomes:| LaTeX Math Block |
|---|
| r(t) = r_w + 2 \sqrt{\chi t} |
This leads to estimation of isobar velocity: | LaTeX Math Block |
|---|
| u_p(t) = \sqrt{\frac{\chi}{t}}
|
|
See Also
Physics / Mechanics / Continuum mechanics / Fluid Mechanics / Fluid Dynamics / Radial fluid flow / Pressure diffusion / Pressure Diffusion @model
Petroleum Industry / Upstream / Subsurface E&P Disciplines / Well Testing / Pressure Testing
[ Well & Reservoir Surveillance ]
[ Line Source Solution (LSS) @model ] [ Linear Flow Pressure Diffusion @model ]
| Show If |
|---|
|
| Panel |
|---|
|
| Expand |
|---|
| but this only works for the middle-times and long-times as early times are influenced by wellbore storage and non-linear effects of skin.
| Expand |
|---|
| | Include Page |
|---|
| Line Source Solution (LSS) |
|---|
| Line Source Solution (LSS) |
|---|
|
|
| LaTeX Math Block |
|---|
| p(t,r) = p_i + \frac{q_t}{4 \pi \sigma} \, {\rm Ei} \bigg( - \frac{r^2}{4 \chi t} \bigg) |
Рассмотрим плоскопараллельный аксиально-симметричный однородный пласт постоянной толщины , с радиальной координатой в перпендикулярной к оси скважины плоскости, который вскрыт бесконечно тонкой скважиной в точке (где – радиальная координата в перпендикулярной к оси скважине плоскости) и начальным пластовым давлением .
Пусть в момент времени
скважина запускается с дебитом (в пересчете на пластовые условия).Диффузия давления описывается решением уравнения однофазного радиального течения в бесконечном однородном пласте: | LaTeX Math Block |
|---|
| \frac{\partial p}{\partial t} = \chi \, \Delta p = \chi \, \frac{1}{r} \frac{\partial}{\partial r} \bigg( r \frac{\partial p}{\partial r} \bigg) |
с начальным условием: | LaTeX Math Block |
|---|
| p(t = 0, r) = p_i |
и граничными условиями: | LaTeX Math Block |
|---|
| p(t, r \rightarrow \infty ) = p_i |
| LaTeX Math Block |
|---|
| anchor | Boundary_q |
|---|
| alignment | left |
|---|
| r \frac{\partial p(t, x )}{\partial r} \bigg|_{r \rightarrow 0} = \frac{q_t}{2 \pi \sigma} |
где | LaTeX Math Inline |
|---|
| body | \sigma = \frac{k \, h}{\mu} |
|---|
|
– гидропроводность пласта, | LaTeX Math Inline |
|---|
| body | \chi = \frac{k}{\mu} \, \frac{1}{\phi \, c_t} |
|---|
|
– пьезопроводность пласта, – проницаемость пласта, – пористость пласта, – сжимаемость пласта, – сжимаемость порового коллектора, – сжимаемость насыщающего пласт флюида, – вязкость насыщающего пласт флюида.
При анализе отклика давления на самой скважине ( ) после включения на достаточно больших временах, удовлетворяющих условию:| LaTeX Math Block |
|---|
| t \gg \frac{r_w^2}{4 \chi}
|
которые на практике наступают очень быстро, можно воспользоваться приближением | LaTeX Math Inline |
|---|
| body | {\rm Ei}(-x) \sim \ln (x) + \gamma \sim \ln (1.781 x) |
|---|
|
, где – постоянная Эйлера.
Режим радиального течения к линейному источнику примет вид:
| LaTeX Math Block |
|---|
| p(t,r_w) = p_i + \frac{q_t}{4 \pi \sigma} \, \ln \bigg( 1.781 \, \frac{r_w^2}{4 \chi t} \bigg) |
Отсюда следует, что уже вскоре после запуска скважины динамическая депрессия на пласт начинает логарифмически расти во времени:
| LaTeX Math Block |
|---|
| \delta p = p_i - p_{wf}(t) \sim { \rm const } + \frac{q_t}{4 \pi \sigma} \, \ln t |
а логарифмическая производная становится постоянной во времени: | LaTeX Math Block |
|---|
| t \frac{d (\delta p)}{dt} \sim \frac{q_t}{4 \pi \sigma} |
В лог-лог координатах лог-производная депрессии будет горизонтальной, что является характерным для радиальной фильтрации в бесконечном пласте.
|
|
|