|
| Fig. 1. Single-barrier well completion schematic |
The Heat Transfer Coefficient (HTC) of dual-barrier well completion is defined by the following equation:
| (1) | \frac{1}{ r_{ci} \, U} = \frac{1}{r_{ci} \, U_{ci}} + \frac{1}{r_{ci} \, U_c} + \frac{1}{r_c \, U_{cem}} |
where
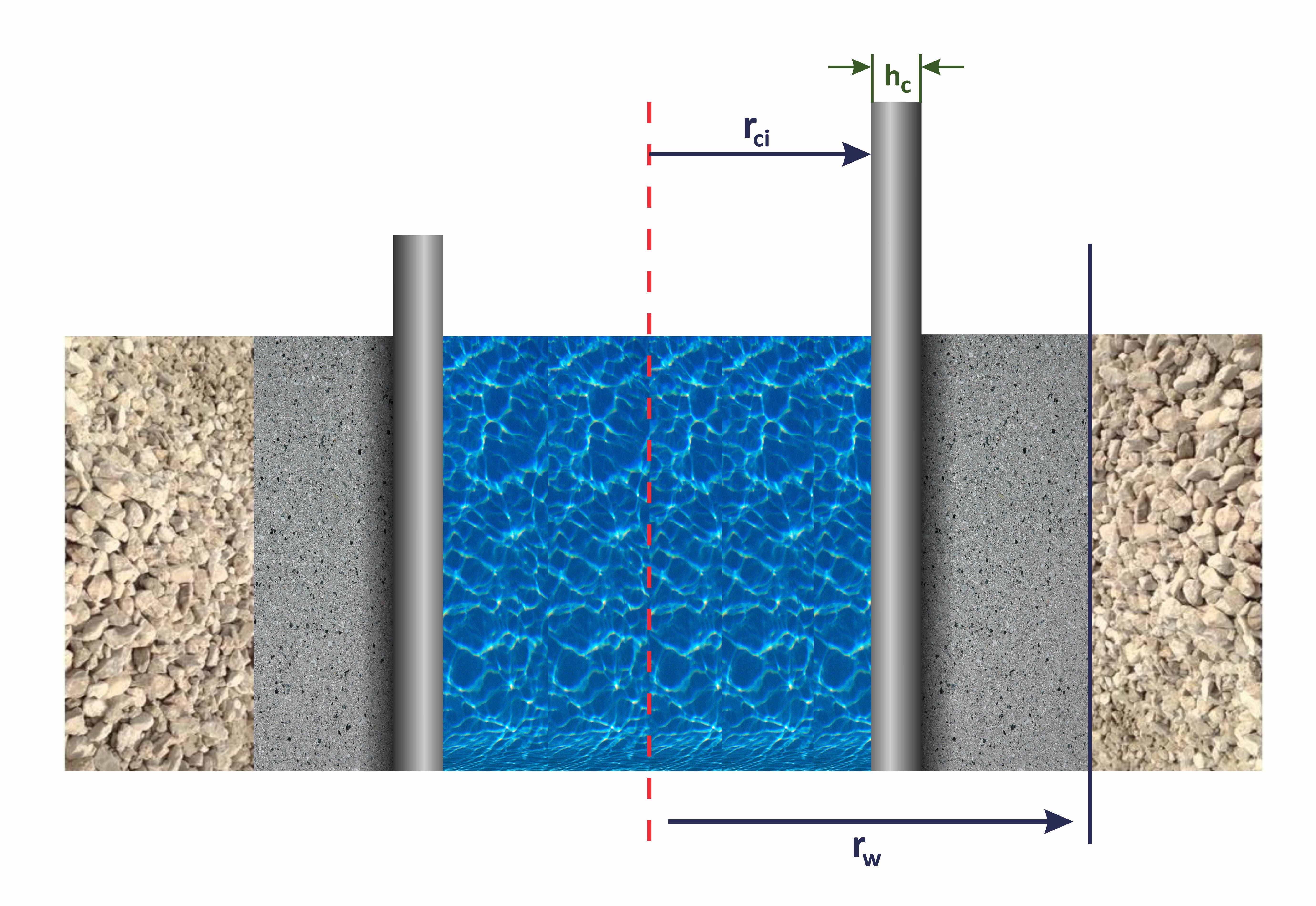
r_c | outer radius of the casing |
r_{ci} | inner radius of the casing |
h_c = r_c - r_i | casing wall thickness |
r_w | wellbore radius by drilling bit |
\displaystyle U_{ci} = \frac{\lambda}{2 \, r_{ci}} \, {\rm Nu}_{ci} | |
\displaystyle U_c = \frac{\lambda_c}{r_{ci} \cdot \ln (r_c/r_{ci})} | Casing Wall Conductive Heat Transfer Coefficient |
\displaystyle U_{cem} = \frac{\lambda_{cem}}{r_c \cdot \ln (r_w/r_c)} | Cement Conductive Heat Transfer Coefficient |
\lambda | thermal conductivity of fluid moving through the tubing |
\lambda_с | thermal conductivity of casing material |
\lambda_{cem} | thermal conductivity of cement |
The equation
(1) can be written explicitly as:
| (2) | \frac{1}{ r_{ti} \, U} = \frac{2}{\lambda \, {\rm Nu}_{ci}} + \frac{1}{\lambda_c} \ln \frac{r_c}{r_{ci}} + \frac{1}{\lambda_{cem}} \ln \frac{r_w}{r_c} |
See also
Physics / Thermodynamics / Heat Transfer / Heat Transfer Coefficient (HTC) / Heat Transfer Coefficient (HTC) @model
[ Dual-barrier well completion Heat Transfer Coefficient @model ]
[ Thermal conductivity ] [ Nusselt number (Nu) ]