Single-well Pressure Pulsation survey
Motivation
One of the most important objectives of the well testing is to assess the drainable hydrocarbon reserves and reservoir properties around tested well.
This particularly becomes important in appraisal drilling as well testing is the only source of this information.
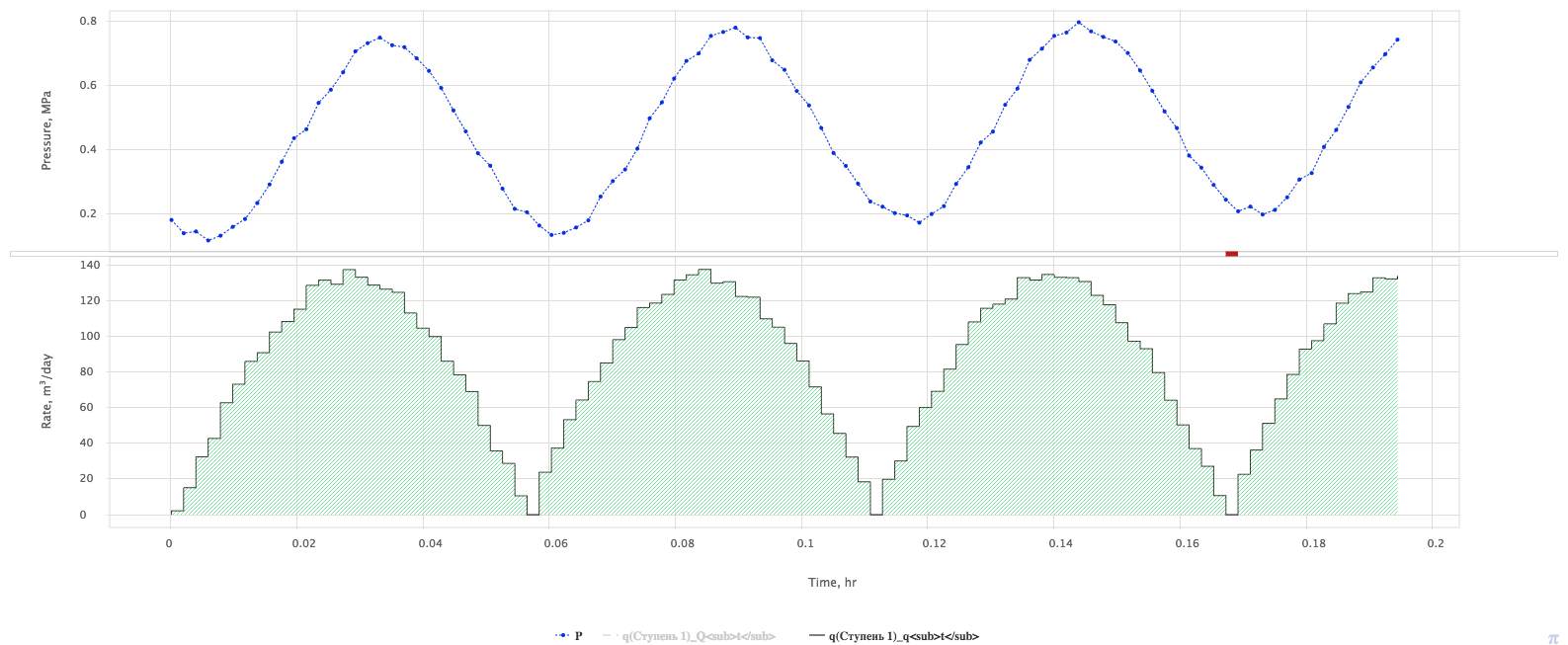
The Self-Pulse Test (SPT) is a single-well pressure test with periodic changes in flow rate and pressure (see Fig. 1).
| Fig. 1. Typical record of pressure and rate variation during SPT |
Objectives
- Assess reservoir volume around well
- Assess reservoir permeability and thickness variation around well
Deliverables
The advantages of SPT deliverables over conventional single-well test is illustrated below.
| Vhc | Potential hydrocarbon reserves |
| Ve | Drainage volume |
| Ae | Drainage area |
| knear | Permeability of the near-reservoir zone |
| hnear | Effective thickness of the near-reservoir zone |
| kfar | Permeability of the far-reservoir zone |
| hfar | Effective thickness of the far-reservoir zone |
| S | Skin-factor |
| Pu(t) | Deconvolution of the long-term unit-rate response |
Inputs
| Property | Description | Data Source |
|---|---|---|
| Bo | Oil Formation Volume Factor | PVT samples / Correlations |
| Bg | Gas Formation Volume Factor | PVT samples / Correlations |
| Bw | Water Formation Volume Factor | PVT samples / Correlations |
| co | Oil compressibility | PVT samples / Correlations |
| cw | Water compressibility | PVT samples / Correlations |
| cg | Gas compressibility | PVT samples / Correlations |
| cr | Rock compressibility | Core samples / Correlations |
| swi | Initial water saturation | Core samples |
\phi | Porosity | Core samples |
Procedure
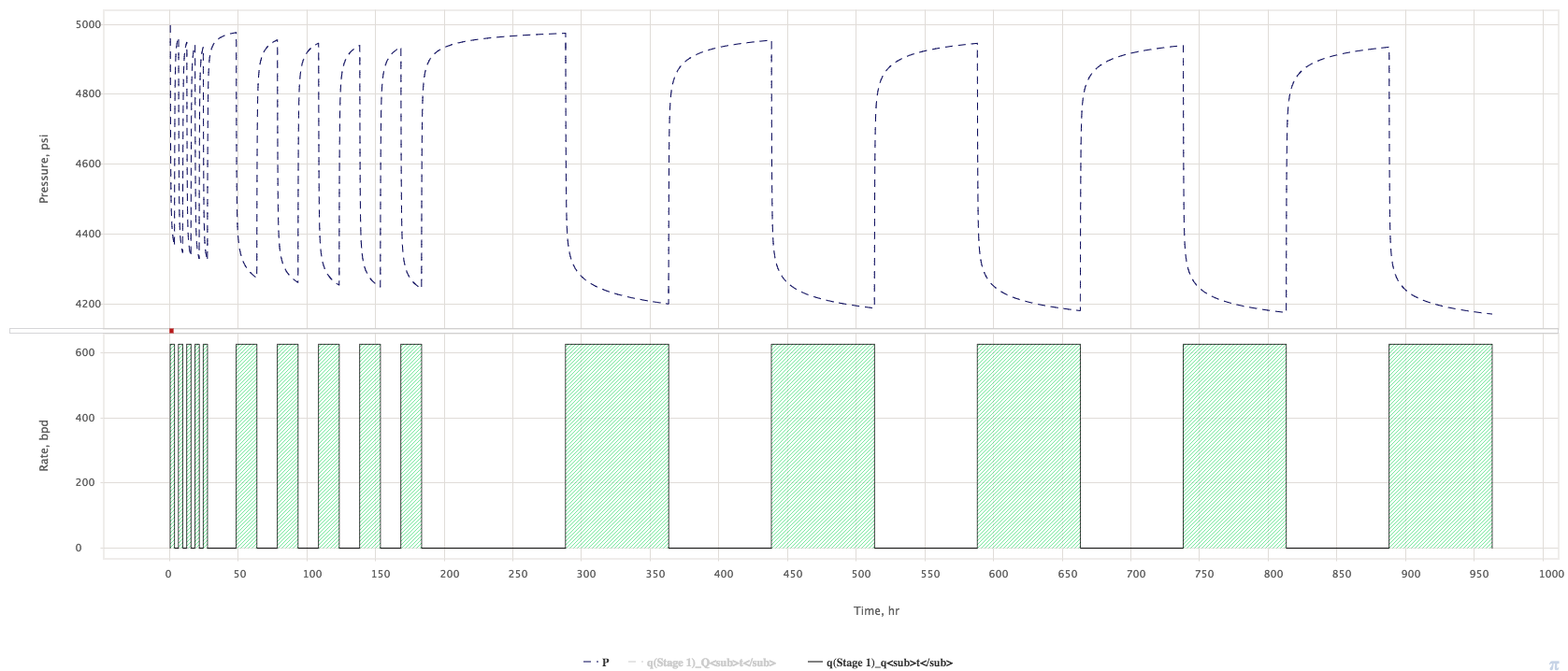
The typical SPT procedure is brought on Fig. 2.
| Fig. 2. Typical SPT procedure |
It normally consists ion three consequent tests with three different cycling frequencies:
- Test 1 = high freq pulsations (5 pulses with period T)
- Test 2 = mid freq pulsations (5 pulses with with period 5T)
- Test 3 = Low freq pulsations (5 pulses with period 25 T)
The total duration of the test is 155 T.
Typically T = 3 hrs and total test duration is around 20 days.
Every pulse includes one choke-up and one choke-down so that full SPT survey require 60 choke operations during 40 days which is a lot of field activity for a given well.
It would be extremely difficult to perform this manually and usual practice is to arrange a programmable remote-controlled flow variation.
Model
Interpretation
Automated flowrate-pressure fata records match in multiphase 2D pressure simulator with:
- Single well and circle boundary
- High density LGR (meters)
- High density time grid (seconds)
See Also
Petroleum Industry / Upstream / Subsurface E&P Disciplines / Well Testing / Pressure Testing / Cased-Hole Pressure Transient Test / Pressure Interference Test (PIT) / Pressure Pulsations Survey
[ Well & Reservoir Surveillance ] [ Drawdown Transient Response (DTR) ] [ Pressure Pulse Propagation ]