Для сжимаемого флюида (газа или жидкости) массой 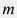 , молярной массой , молярной массой 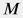 объемом объемом 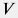 , находящейся при температуре , находящейся при температуре 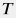 и давлении и давлении 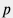 вводится понятие Z-фактора вводится понятие Z-фактора Z = \frac{pV}{\nu RT} = \frac{pV M}{m RT} |
где 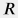 универсальная газовая постоянная и универсальная газовая постоянная и  – количество молей флюида. – количество молей флюида.
Зависимость величины 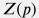 от давления определяется в лабораторных данных, а также может быть предсказана на основе компонентного состава или популярных корреляций. от давления определяется в лабораторных данных, а также может быть предсказана на основе компонентного состава или популярных корреляций.
Плотность флюида выражается через Z-фактор как \rho = \frac{M}{RT} \frac{p}{Z} |
а сжимаемость c = \frac{1}{\rho} \frac{d \rho}{dp} = \frac{1}{p} - \frac{1}{Z} \frac{dZ}{dp} |
Рассмотрим уравнение непрерывности  в общем виде: в общем виде: \frac{\partial ( \rho \phi)}{\partial t} + \nabla \cdot ({\rho \bf u}) = q_m(t, {\bf r}) = \rho q(t, {\bf r}) |
и подставим уравнение движения (обобщенный Дарси) \frac{\partial ( \rho \phi)}{\partial t} + \nabla \cdot \bigg( \rho \, \frac{k}{\mu} \nabla p \bigg) = \rho q(t, {\bf r}) |
Подставляя выражение для плотности получим уравнение пьезодинамики: \frac{\partial}{\partial t} \bigg( \frac{p}{Z} \phi \bigg) + \nabla \cdot \bigg( k \, \frac{p}{\mu Z} \nabla p \bigg) = \rho q(t, {\bf r}) |
Вычисляя производную по времени явно: \frac{\partial}{\partial t} \bigg( \frac{p}{Z} \phi \bigg) = \bigg( \frac{p}{Z} \frac{d\phi}{dp} + \phi \frac{d}{dp} \bigg( \frac{p}{Z} \bigg) \bigg) \frac{\partial p}{\partial t} =
\bigg( \frac{p}{Z} \, c_r \phi + \phi \bigg( \frac{1}{Z} - \frac{p}{Z^2} \frac{dZ}{dp} \bigg) \bigg) \frac{\partial p}{\partial t}=
\frac{\phi p}{Z} \bigg( c_r + \frac{1}{p} - \frac{1}{Z} \frac{dZ}{dp} \bigg) \frac{\partial p}{\partial t}=
\frac{\phi p}{Z} ( c_r + c ) \frac{\partial p}{\partial t}=
\frac{\phi p}{Z} c_t \frac{\partial p}{\partial t}
|
и уравнение пьезодинамики принимает вид: \frac{\phi c_t p}{Z} \frac{\partial p}{\partial t} + \nabla \cdot \bigg( k \, \frac{p}{\mu Z} \nabla p \bigg) = \rho q(t, {\bf r}) |
Рассмотрим случай, когда проницаемость зависит от давления и не зависит от градиента давления:  , где , где  – пространственное распределение абсолютной проницаемости, – пространственное распределение абсолютной проницаемости,  – динамиечский параметр, характеризующий зависимость абсолютной проницаемости от давления и равный единице при начальном пластовом давлении: – динамиечский параметр, характеризующий зависимость абсолютной проницаемости от давления и равный единице при начальном пластовом давлении:  . .
Тогда уравнение пьезодинамики принимает вид: \frac{\phi c_t p}{Z} \frac{\partial p}{\partial t} + \nabla \cdot \bigg( k_0 \, \frac{p \, \xi}{\mu Z} \nabla p \bigg) = \rho q(t, {\bf r}) |
или \frac{\mu \phi c_t}{\xi} \frac{p \,\xi}{\mu Z} \frac{\partial p}{\partial t} + \nabla \cdot \bigg( k_0 \, \frac{p \, \xi}{\mu Z} \nabla p \bigg) = \rho q(t, {\bf r}) |
Введем понятие псевдодавления  : :
\psi = H(p) = \int \frac{p \,\xi(p)}{\mu Z} dp |
Тогда уравнение пьезодинамики принимает вид: \frac{\mu \phi c_t}{\xi} \frac{\partial \psi}{\partial t} + \nabla \cdot \bigg( k_0 \, \nabla \psi \bigg) = \rho q(t, {\bf r}) |
Решение ищется в отношении функции  и впоследствии само давление и впоследствии само давление  находится из уравнения находится из уравнения  где функция где функция  уже считается известной. уже считается известной. Решение уравнения  как правило не представляет труда. Входящие в подынтегральное выражение величины рассчитываются на основе известной модели проницаемости и PVT и, следовательно, интеграл может быть табулирован один раз в широком пределе изменения аргумента (давления), а уравнение как правило не представляет труда. Входящие в подынтегральное выражение величины рассчитываются на основе известной модели проницаемости и PVT и, следовательно, интеграл может быть табулирован один раз в широком пределе изменения аргумента (давления), а уравнение  представляет табличное соотношение между двумя числовыми массивами представляет табличное соотношение между двумя числовыми массивами \psi = H(p) = \int \frac{p \,\xi(p)}{\mu(p) Z(p)} dp \quad \longrightarrow \quad \psi \leftrightarrow p |
и значение одного через другое легко находится, например, методом интерполяции. Обратим внимание, что уравнение  в общем случае не является линейным, так как коэффициент перед производной по времени может сильно зависеть от давления (и соотвественно от псевдодавления). Это наводит на мысль устранить нелинейный коэффициент путем замены временной переменной. в общем случае не является линейным, так как коэффициент перед производной по времени может сильно зависеть от давления (и соотвественно от псевдодавления). Это наводит на мысль устранить нелинейный коэффициент путем замены временной переменной. Введем понятие псевдовремени 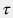 , которое связано с реальным временем как некая функция , которое связано с реальным временем как некая функция  : : t = F(\tau) = \int_0^\tau \frac{\mu(p) \phi(p) c_t(p)}{\xi(p)} d\tau |
которое в каждой точке пласта может течь по разному  из-за разного поведения давления в окрестности этих точек. из-за разного поведения давления в окрестности этих точек.
Тогда уравнение пьезодинамики принимает вид: \frac{\partial \psi}{\partial \tau} + \nabla \cdot \bigg( k_0 \, \nabla \psi \bigg) = \rho q(t, {\bf r}) |
и представляет собой линейное дифференциальное уравнение на функцию  . . Однако правая часть уравнения сохранила выражения через реальные давления и время, что не позволяет замкнуть уравнение на неизвестную функцию  . . Плотность флюида 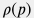 , как функция давления, может быть однозначно выражена как функция псевдодавления , как функция давления, может быть однозначно выражена как функция псевдодавления  на основе табуляции на основе табуляции  . . Сложнее обстоит дело с дебитом  , так как исходные данные о дебите представлены в реальном времени, а связь между реальным временем и псевдовременем может быть установлена только после нахождения псевдодавления от псевдовремени , так как исходные данные о дебите представлены в реальном времени, а связь между реальным временем и псевдовременем может быть установлена только после нахождения псевдодавления от псевдовремени  . . В этом случае необходимо идти на компромисс и вначале установить прокси-связь между временем и псевдовременем в точке расположения тестовой скважины. Если известны показания манометра  в процессе теста, то эти данные подставляются в формулу в процессе теста, то эти данные подставляются в формулу  и формируется прокси-связь между реальным временем и приборным-псевдовременем и формируется прокси-связь между реальным временем и приборным-псевдовременем  . По этой связи дебиты скважин пересчитываются на приборное псевдовремя . По этой связи дебиты скважин пересчитываются на приборное псевдовремя  , которое приближенно полагается соответствующим истинному псевдо-времени , которое приближенно полагается соответствующим истинному псевдо-времени  и тем самым уравнение и тем самым уравнение \frac{\partial \psi}{\partial \tau} + \nabla \cdot \bigg( k_0 \, \nabla \psi \bigg) = \rho(\psi) q(\tau, {\bf r}) |
становится замкнутым относительно неизвестной функции  . . Если же данных о записи давления на тестовой скважине нет и решается задача прямого моделирования, то задачу можно решать итерационно, вначале полагая псевдовремя линейно пропорциональным реальному времени (то есть приняв что все подинтегральные величины в  константы и рассчитаны при стартовом значении давления константы и рассчитаны при стартовом значении давления  ): ): \tau_{\rm sim} = \frac{\xi(p_0)}{\mu(p_0) \phi(p_0) c_t(p_0)} \, t |
Алгоритм нахождения поля давления выглядит следующим образом: - Уравнение
 решается численно и находится табулированная функция решается численно и находится табулированная функция  . . - Каждому значению функции
 приводится в соответствие значение функции приводится в соответствие значение функции  на основе табуляции на основе табуляции  . . - Полученные значения
 подставляются в подынтегральное выражение подставляются в подынтегральное выражение  и для ранжира значений псевдовремени и для ранжира значений псевдовремени 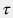 рассчитывается массив значений реального времени рассчитывается массив значений реального времени 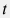 . . - По полученной таблице соответствия времен
 функция давления от псевдовремени пересчитывается в реальное время функция давления от псевдовремени пересчитывается в реальное время  что и дает решение исходной нелинейной задачи что и дает решение исходной нелинейной задачи  . .
В случае неоднородного коллектора, принципиальным вопросом метода псевдопотенциалов является выбор точки 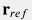 в пространстве где будет взяты пористость в пространстве где будет взяты пористость  и сжимаемость и сжимаемость   , для расчета псевдовремени , для расчета псевдовремени  . Этот выбор зависит от целей моделирования. Для оценки ранних времен надо выбирать . Этот выбор зависит от целей моделирования. Для оценки ранних времен надо выбирать 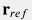 из окрестности скважины, а для оценки поздних времен необходимо усреднять значения пористости и сжимаемости по большой области (соответствующей радиусу сканирования пласта в рамках теста). из окрестности скважины, а для оценки поздних времен необходимо усреднять значения пористости и сжимаемости по большой области (соответствующей радиусу сканирования пласта в рамках теста).
Еще раз заметим, что данный подход не покрывает модели с зависимостью проводимости пласта от депрессии (например нелинейный Дарси или начальный градиент сдвига).
| can be considered as constant in time which makes Pseudo-Time being proportional to freagular time:
can not be considered as constant in time which leads to distortion of pressure transient diagnostics at early times.
:
, viscosity does not depend on pressure
and total compressibility is fully defined by fluid compressibility
which simplifies the expression for Pseudo-Pressure and Pseudo-Time as to: