Motivation
In many practical cases the reservoir flow created by well or group of wells is getting aligned with a specific linear direction away from well.
This happens when well is placed in a channel or a narrow compartment. It also happens around fracture planes and conductive faults.
This type of flow is called linear fluid flow and a type library model provides a reference for linear fluid flow diagnostics.
Inputs & Outputs
| Inputs | Outputs | ||
|---|---|---|---|
q_t | total sandface rate | p(t,x) | reservoir pressure |
p_i | initial formation pressure | p_{wf}(t) | well bottomhole pressure |
d | reservoir channel width | ||
\sigma | transmissibility | ||
\chi | pressure diffusivity | ||
Physical Model
| Constant rate production | q_t = \rm const |
| Linear fluid flow | p(t, x) |
| Slightly compressible fluid flow | c_t(p) = c_r +c = \rm const |
| Homogeneous reservoir | M(x, p)=M =\rm const \phi(x, p)=\phi =\rm const h(x)=h =\rm const |
| Infinite boundary | x \rightarrow \infty |
Mathematical Model
Scope of Applicability
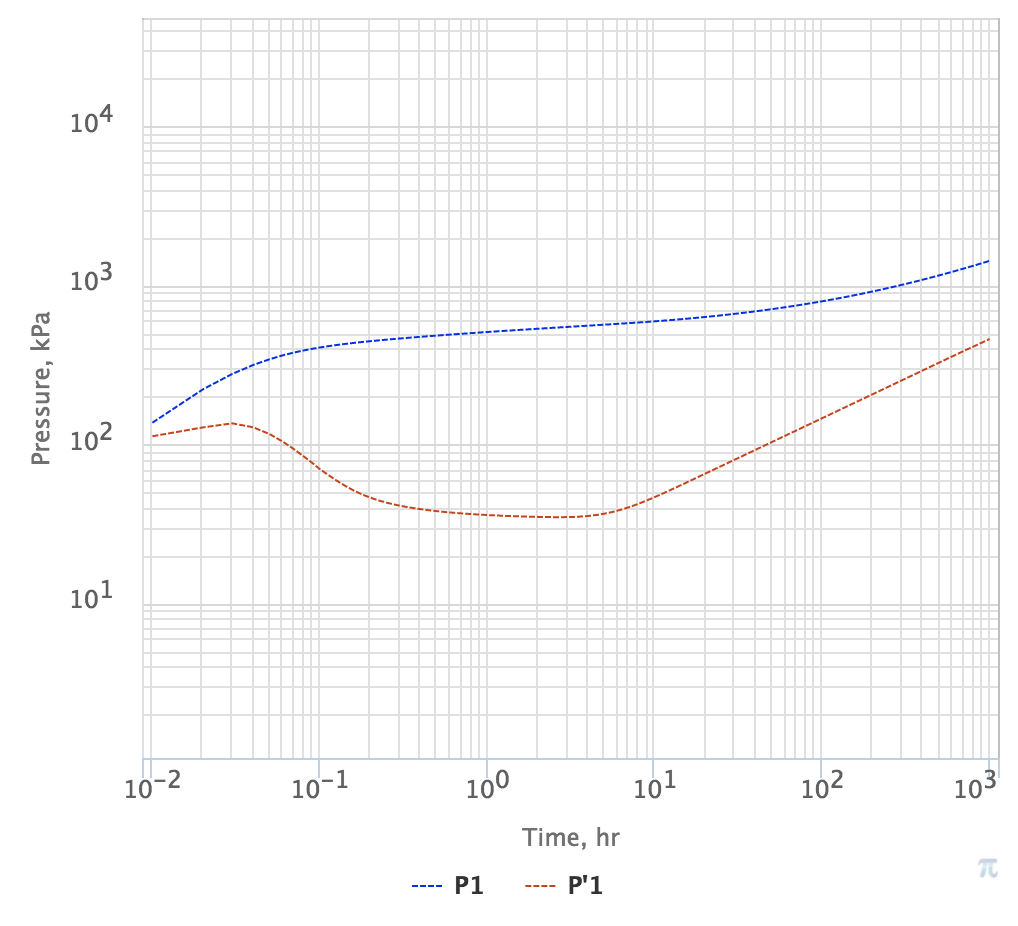
Pressure Testing – Channel or Narrow compartment reservoir
Pressure Drop |
| |||
Log derivative |
| |||
| Fig. 2. PTA Diagnostic plot for linear fluid flow in reservoir channel |
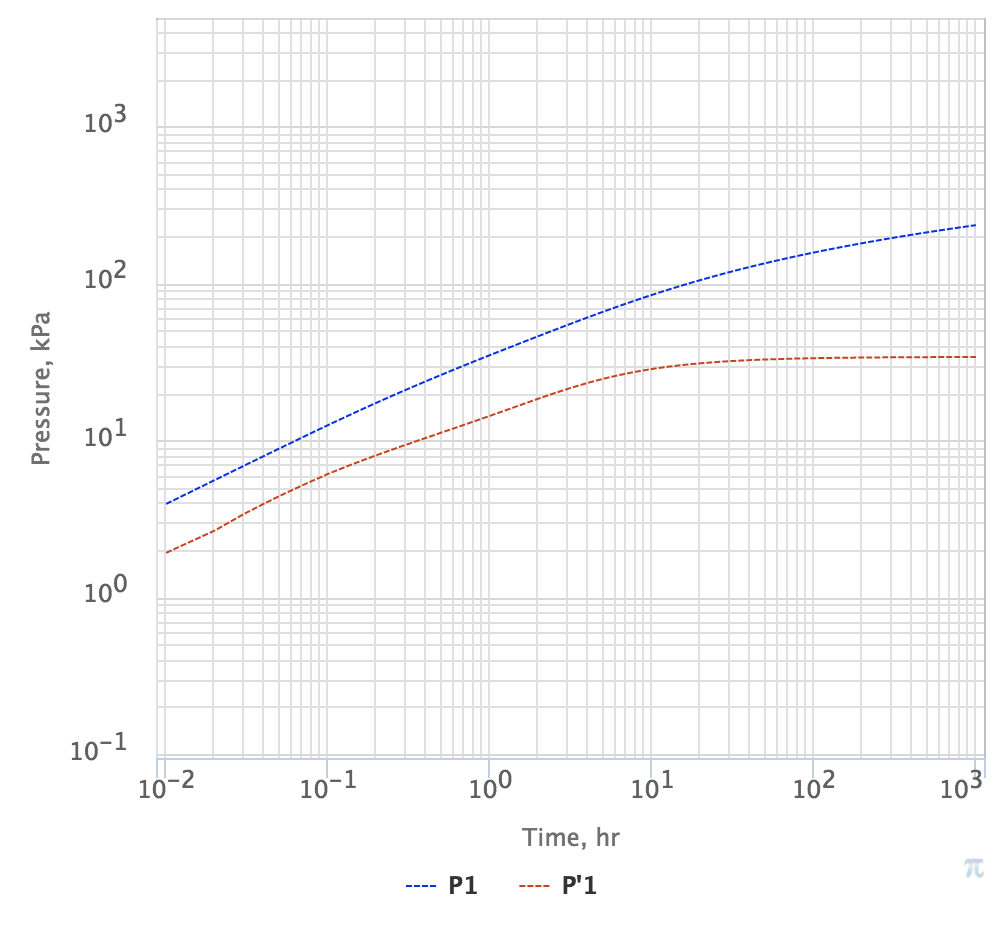
Pressure Testing – Infinite conductivity fracture
Pressure Drop |
| |||
Log derivative |
| |||
| Fig. 2. PTA Diagnostic plot for linear fluid flow in infinite conductivity fracture |
See also
Physics / Fluid Dynamics / Linear fluid flow