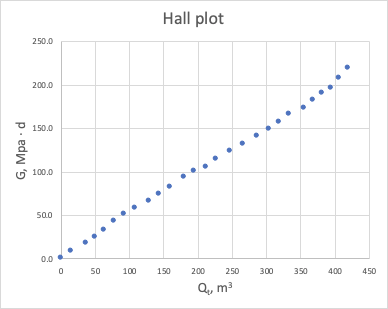
Synonym: Cumulative Productivity Plot = Hall Plot
One of the Productivity Diagnostics methods based on correlation between cumulative pressure drawdown:
| (1) | G (t) = \int_0^t \left( p_{wf}(\tau) - p_e(\tau) \right) d\tau |
and total sandface cumulative offtake/intake:
| (2) | Q_t(t) = \int_0^t q_t(\tau) d\tau |
where
\tau | production/injection time |
q_t | total sandface flowrate as function of time \tau |
p_e | drain-area formation pressure as function of time \tau |
p_{wf} | bottomhole pressure as function of time \tau |
| Fig. 1. Hall Plot |
It shows unit slope on log-log plot for stabilized reservoir flow:
| (3) | G(t) = J^{-1} Q_t(t) |
where
J | constant productivity index |
Due to integration procedure the Hall Plot has a better tolerance to uncertainties in formation pressure and bottomhole pressure comparing to Unweighted J-plot and usually results in more accurate estimation of productivity index.
It is highly recommended to plot sandface flowrates rather than surface flowrates to achieve better linearity in correlation for stabilized reservoir flow.
Although it is equally applicable to producers and injectors, due to lack of BHP and formation pressure data availability for producers in most practical cases in the past the Hall plot analysis was mostly applied for water injectors.
The pressure drawdown integral G(t) is usually calculated over interpolated values of formation pressure and bottomhole pressure :
| G(t) = \int_0^t \left( p_{wf}(\tau) - p_e(\tau) \right) d\tau = \sum_k \left( p_{wf}(\tau_k) - p_e(\tau_k) \right) \delta \tau_k |
See Also
Petroleum Industry / Upstream / Production / Subsurface Production / Field Study & Modelling / Production Analysis / Productivity Diagnostics