Motivation
Assume the well is producing q_w of water, q_o of oil and q_g of gas as measured daily at separator with pressure p_s and temperature T_s.
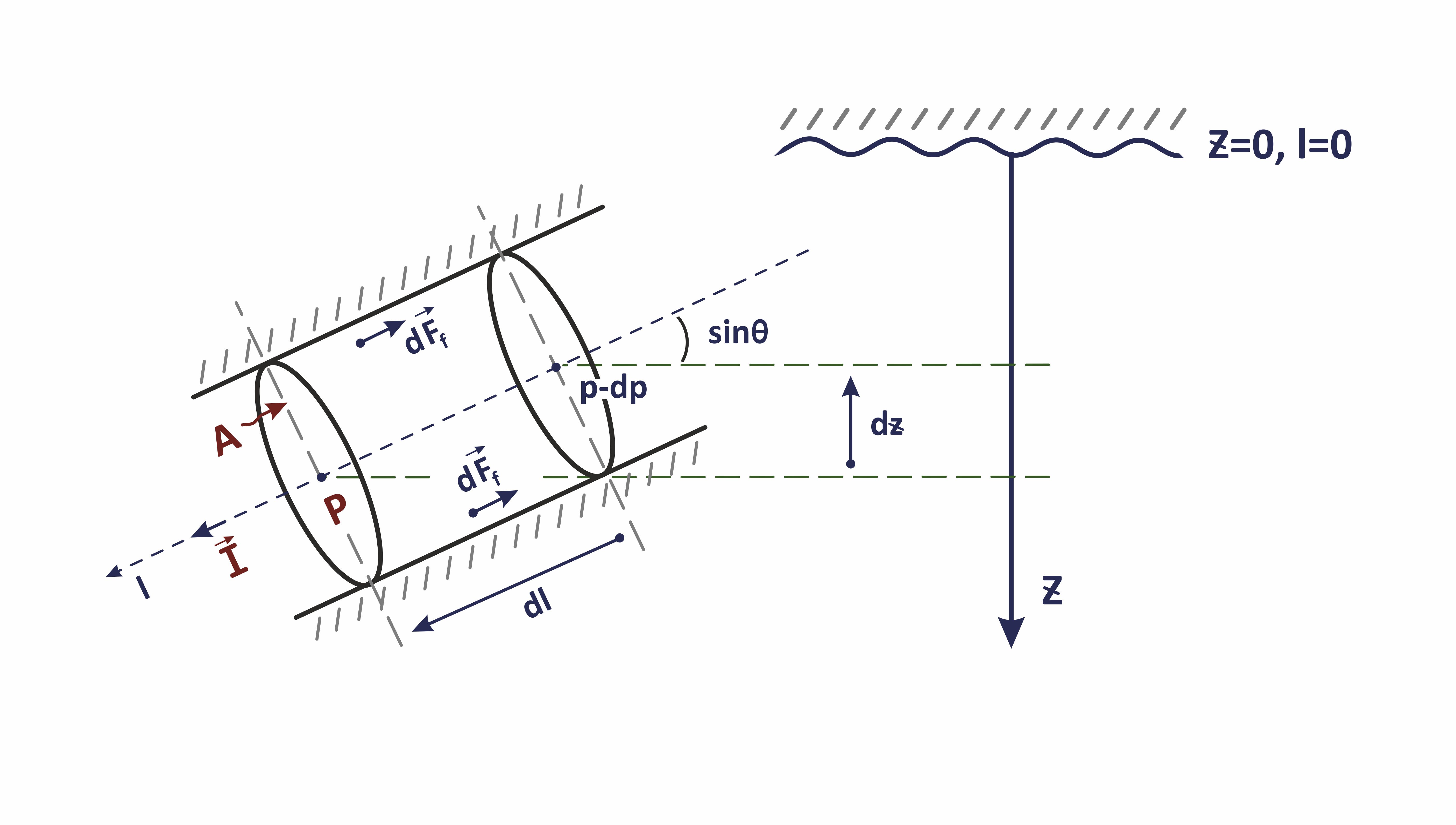
While going down to depth l along the hole the wellbore pressure P_{wf}(l) will be growing due to gravity of fluid column and friction losses emerging from fluid contact with inner pipe walls .
Wellbore temperature T(l) will be also varying due to heat exchange with surrounding rocks.
The volume shares \{ s_w(l), \, s_o(l), \, s_g(l) \}, occupied by different phases will be varying along hole due to along-hole pressure-temperature variation, phase segregation and phase slippage.
It is now possible to simulate the stationary multiphase wellbore flow and link the surface flow conditions (pressure, temperature and rates) to downhole flow conditions at any depth.
The most adequate and practical model can be built for a stationary fluid flow at hydrodynamic and thermodynamic equilibrium.
If flow is changing slowly over time the same solutions can be used with inputs as time functions which is called quasi-stationary flow conditions.
This model finds important applications in industry.
If well production has been changed abruptly (for example opening or closing the flow) there will be a transition period towards the new quasi-stationary flow conditions (usually minutes or few hours).
The transition period for pressure and temperature is different and wellbore temperature takes much longer time to stabilize than pressure.
Unlike single-phase flow (Wellbore Water Flow and Wellbore Gas Flow) the complexity of the multiphase flow during transition is so high and unstable that building a simple mathematical model does not make a practical sense.
Definition
Mathematical model of Multiphase Wellbore Flow predicts the temperature, pressure and flow speed distribution along the wellbore trajectory with account for:
- tubing head pressure which is controled by gathering system or injection pump
- wellbore design (pipe diameters, pipe materials and inter-pipe annular fillings)
- fluid friction with tubing /casing walls
- interfacial phase slippage
- heat exchange between wellbore fluid and surrounding rocks via complex well design
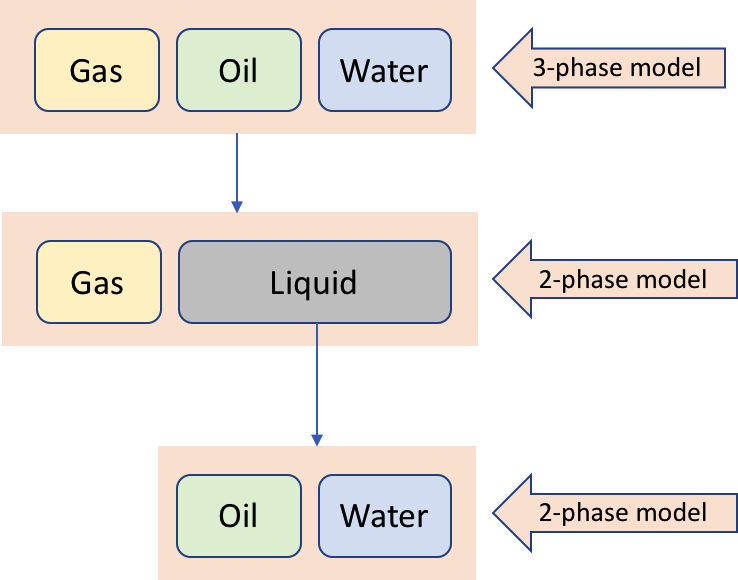
Consider a 3-phase water-oil-gas flow: \alpha = \{ w, \, o, \, g \}.
The \alpha-phase volumetric flow fraction ( also called phase cut or input hold-up or no-slip hold-up ) is defined as:
| (1) | \gamma_\alpha = \frac{q_\alpha}{q_t} |
where q_\alpha – volumetric flow rate of \alpha-phase and q_t is the total volumetric fluid production rate:
| (2) | q_t = \sum_\alpha q_\alpha = q_w + q_o + g_g |
In multiphase wellbore flow each phase occupies its own area A_\alpha of the total cross-sectional area A of the lifting pipe.
This area can be connected into a single piece of cross-sectional area (like in case of slug or annular flow) or dispersed into a number of connected spots (like in case of bubbly flow).
A share of total pipe cross-section area occupied by moving \alpha-phase is called an \alpha-phase in-situ hold-up and defined as:
| (3) | s_\alpha = \frac{A_\alpha}{A} |
so that a sum of all in-situ hold-ups is subject to natural constraint:
| (4) | \sum_\alpha s_\alpha = s_w + s_o + s_g = 1 |
When word hold-up is used alone it usually means in-situ hold-up and should not be confused with input hold-up or no-slip hold-up which should be better called volumetric flow fraction.
The actual average cross-sectional velocity of moving \alpha-phase is called in-situ velocity and defined as:
| (5) | u_\alpha = \frac{q_\alpha}{A_\alpha} |
where q_\alpha is the volumetric \alpha-phase flowrate through cross-sectional area A_\alpha.
The superficial velocity of \alpha-phase is defined as the
| (6) | u_{s \alpha} = \frac{q_\alpha}{A}= s_\alpha \cdot u_\alpha |
The multiphase mixture velocity is defined as total flow volume normalized by the total cross-sectional area:
| (7) | u_m = \frac{1}{A} \sum_\alpha q_\alpha = \sum_\alpha u_{s \alpha} = \sum_\alpha s_\alpha \cdot u_\alpha |
The difference between velocities of \alpha_1-phase and \alpha_2-phase is called interfacial phase phase slippage:
| (8) | u_{\alpha_1 \alpha_2} = u_{\alpha_1} - u_{\alpha_2} |
The multiphase fluid density \rho_m is defined by exact formula:
| (9) | \rho_m = \sum_\alpha s_\alpha \rho_\alpha |
where \rho_\alpha – density of \alpha-phase.
The two-phase gas-liquid model is defined in the following terms:
| (10) | u_m = u_{s g} + u_{s l} = s_g u_g + (1-s_g) u_l |
The two-phase oil-water model is defined in the following terms:
| (11) | u_m = u_{s o} + u_{s w} = s_o u_o + (1-s_o-s_g) u_w |
The 3-phase water-oil-gas model is usually built as a superposition of gas-liquid model and then oil-water model:
Input & Output
| Input | Output |
|---|---|
p_s, \, T_s, \ \{ q_w, q_o, \, q_g \} as values at separator | p(l), \, T(l), \, \{ s_w(l), \, s_o(l), \, s_g(l) \}, \, \{ q_w(l), \, q_o(l), \, q_g(l) \} as logs along hole |
Application
| Activity | Input | Output | ||
|---|---|---|---|---|
| 1 | WPA – Well Performance Analysis | Optimizing the lift performance based on the IPR vs VLP models | p_s, \, T_s, \ \{ q_w, q_o, \, q_g \} as values at separator | p_{wf}(l = l_{datum}) as value at formation datum |
| 2 | DM – Dynamic Modelling | Relating production rates at separator to bottom-hole pressure with VLP | p_s, \, T_s, \ \{ q_w, q_o, \, q_g \} as values at separator | p_{wf}(l = l_{datum}) as value at formation datum |
| 3 | PRT – Pressure Testing | Adjust gauge pressure to formation datum | p_{wf}(l = l_{gauge}) as value at downhole gauge | p_{wf}(l = l_{datum}) as value at formation datum |
| 4 | PLT – Production Logging | Interpretation of production logs | \{ p(l), \, T(l), \, u_m(l), \, s_w(l), \, s_o(l), \, s_g(l) \} as logs along hole | \{ q_w(l), \, q_o(l), \, q_g(l) \} as logs along hole |
| 5 | RFP – Reservoir Flow Profiling | Interpretation of reservoir flow logs | \{ p(l), \, T(l), \, u_m(l), \, s_w(l), \, s_o(l), \, s_g(l) \} as logs along hole | \{ q_w(l), \, q_o(l), \, q_g(l) \} as logs along hole |
Mathematical Model
Homogeneous Model
The multiphase homogeneous wellbore flow model assumes that fluid is at stationary hydrodynamic and thermodynamic equilibrium and there is no slip between phases.
This means that all have the same temperature:
| (12) | T_w = T_o = T_g = T |
same pressure:
| (13) | P_w = P_o = P_g = T |
same velocity:
| (14) | u_w = u_o = u_g = u_m |
and all dynamic fluid parameters are constant in time:
| (15) | \frac{\partial T}{\partial t} = 0, \quad \frac{\partial P}{\partial t} = 0, \quad \frac{\partial u_m}{\partial t} = 0 |
The model is defined by the following set of 1D equations:
| (16) | A(l) \rho_m u_m = \rho_{sm} q_{s} = \rm const |
| (17) | \frac{dp}{dl} = - \rho_m u_m \frac{\partial u_m}{\partial l} + \rho_m \, g \, \cos \theta + \frac{ f_m \, \rho_m \, u_m^2 \, }{2 d} |
| (18) | \sum_\alpha \big( \rho_\alpha \, c_{p \, \alpha} \big) \ q_m \ \frac{\partial T}{\partial l} \ = \ \sum_\alpha \rho_\alpha \ c_{p \alpha} T_\alpha \frac{\partial q_\alpha}{\partial l} |
The right side of equation (18) represents the heat inflow resulting from the fluid flow from reservoir into a wellbore which carries the original reservoir temperature T_r with heating/cooling effect from reservoir-flow throttling and well-reservoir contact throttling:
| (19) | T_\alpha = T_r + \epsilon_\alpha \, \delta p = T_r + \epsilon_\alpha \, (p_e - p) |
The discrete computational scheme for (18) will be:
| (20) | \bigg( \sum_\alpha \rho_\alpha^{k-1} \ c_{p \alpha}^{k-1} \ q_\alpha^{k-1} \bigg) T^{k-1} - \bigg( \sum_\alpha \rho_\alpha^k \ c_{p \alpha}^k \ q_\alpha^k \bigg) T^k = \sum_\alpha \rho_\alpha^k \ c_{p \alpha}^k \ (q_\alpha^{k-1} - q_\alpha^k) \, (T_r^k + \epsilon_\alpha^k \delta p^k ) |
where \delta p^k = p_e^k - p_{wf}^k is drawdown, p_e^k – formation pressure in k-th grid layer, p_{wf}^k – bottom-hole pressure across k-th grid layer, T_r^k – remote reservoir temperature of k-th grid layer.
The l-axis is pointing downward along hole with (k-1)-th grid layer sitting above the k-th grid layer.
If the flowrate is not vanishing during the stationary lift ( \sum_{a = \{w,o,g \}} |q_\alpha^{k-1}| > 0) then T^{k-1} can be calculated iteratively from previous values of the wellbore temperature T^k as:
| (21) | T^{k-1} = \frac{\bigg( \sum_\alpha \rho_\alpha^k \ c_{p \alpha}^k \ q_\alpha^k \bigg) T^k + \sum_\alpha \rho_\alpha^k \ c_{p \alpha}^k \ (q_\alpha^{k-1} - q_\alpha^k) \, (T_r^k + \epsilon_\alpha^k \delta p^k )}{\bigg( \sum_\alpha \rho_\alpha^{k-1} \ c_{p \alpha}^{k-1} \ q_\alpha^{k-1} \bigg) } |
Slippage Model
The multiphase slippage wellbore flow model assumes that fluid is at hydrodynamic and thermodynamic equilibrium and there is a slip between phases so that phases may be moving with different flow speeds u_w \neq u_o \neq u_g.
The model is defined by the following set of 1D equations:
| (22) | A(l) \sum_\alpha \rho_\alpha u_\alpha = \sum_\alpha \rho_{s\alpha} q_{s\alpha} = \rm const |
| (23) | \sum_\alpha \rho_\alpha u_\alpha \frac{\partial u_\alpha}{\partial l} = - \frac{dp}{dl} + \rho_m \, g \, \cos \theta + \frac{ f_m \, \rho_m \, u_m^2 \, }{2 d} |
| (24) | \sum_\alpha \rho_\alpha \ c_{p \alpha} \ u_\alpha \frac{\partial T}{\partial l} \ = \ \frac{1}{A} \ \sum_\alpha \rho_\alpha \ c_{p \alpha} T_\alpha \frac{\partial q_\alpha}{\partial l} |
It carries the original reservoir temperature with heating/cooling effect from reservoir-flow throttling and well-reservoir contact throttling:
| (25) | T_\alpha = T_r + \epsilon_\alpha \, \delta P = T_r + \epsilon_\alpha \, (P_e - P_{wf}) |
see Nomenclature below.
References
Nomenclature
\mathbf{r} = (x, \ y, \ z) | position vector at which the flow equations are set | ||
(t,x,y,z) | time and space corrdinates , z -axis is orientated towards the Earth centre, (x,y) define transversal plane to the z -axis | ||
l (x, \ y, \ z) | measured depth along wellbore trajectory dl^2 = dx^2 + dy^2 + dz^2 starting from tubing head l (x = x_0, \ y=y_0, \ z = z_{THP}) = 0 | ||
m | indicates a mixture of fluid phases | ||
\alpha = \{w,o,g \} | water, oil, gas phase indicator | \epsilon_\alpha (p, T) | differential Joule–Thomson coefficient of \alpha-phase fluid |
p_s | pressure at separator | \eta_{s \alpha}(p,T) | differential adiabatic coefficient of \alpha-phase fluid |
T_s | temperature at separator | f_m(u_m) | Darcy friction factor at fluid velocity u_m |
p(t, l) | wellbore fluid pressure | d(l) | cross-sectional average pipe flow diameter |
T(t, l) | wellbore fluid temperature | A(l) | cross-sectional area A(l) = 0.25 \, \pi \, d^2(l) |
q_\alpha(t, l) = \frac{d V_\alpha}{dt} | volumetric flow rate \alpha-phase fluid at wellbore depth l | \theta(l) | wellbore trajectory inclination to horizon |
u_\alpha(l) | in-situ velocity of \alpha-phase fluid flow | g = 9.81 \ \rm m/s^2 | gravitational acceleration constant |
\rho_\alpha(p, T) | \alpha-phase fluid density at pressure p and temperature T | \lambda_t(p,T,s_w, s_o, s_g) | effective thermal conductivity of the rocks with account for multiphase fluid saturation |
\rho_m(l) | cross-sectional average fluid density | \lambda_r(p,T) | rock matrix thermal conductivity |
kinematic viscosity of \alpha-phase | \lambda_\alpha(p,T) | thermal conductivity of
\alpha-phase fluid | |
dynamic viscosity of \alpha-phase fluid | \rho_r(p,T) | rock matrix mass density | |
specific isobaric heat capacity of \alpha-phase fluid | c_{pr}(p,T) | specific isobaric heat capacity of the rock matrix | |