Motivation

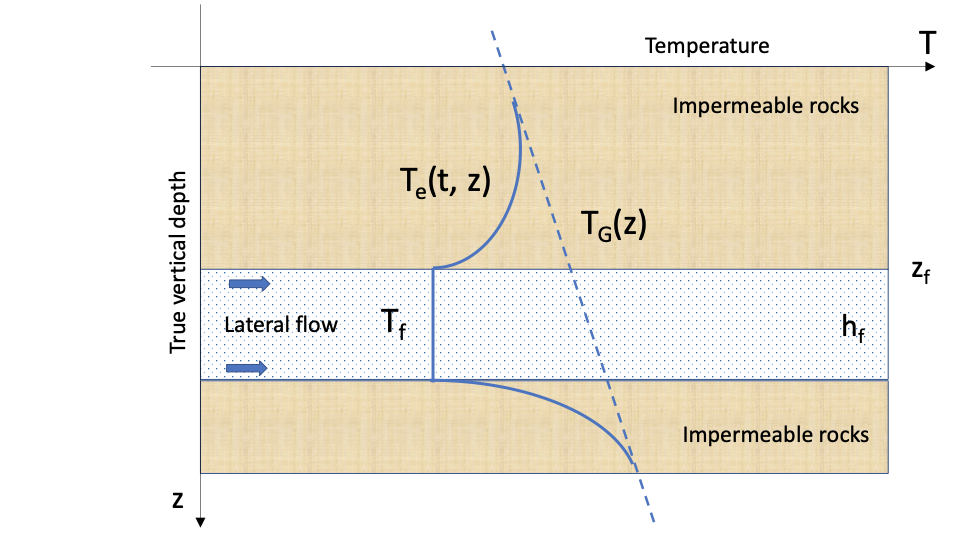
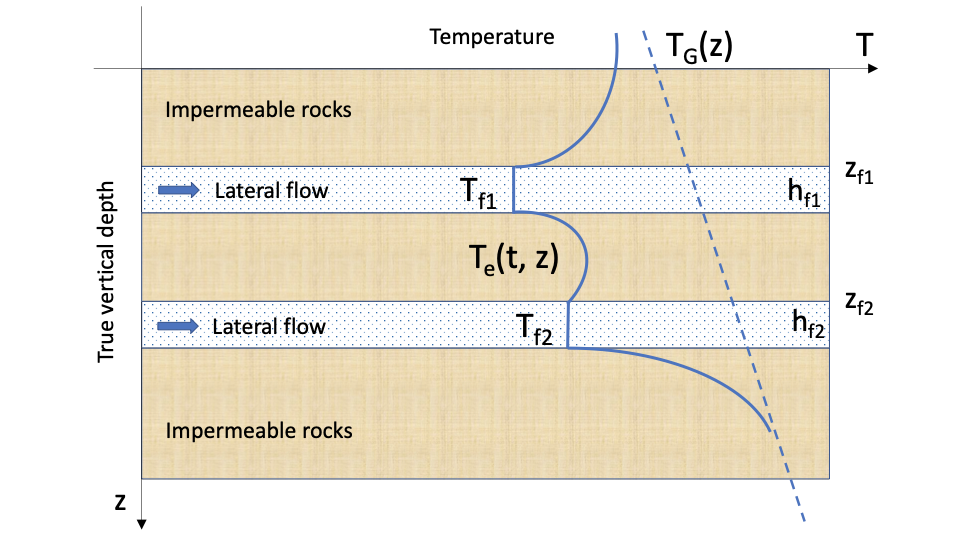
Subsurface Temperature Profile around Lateral Flow makes adjustments to Geothermal Temperature Profile $\begin{array}{l}T_G(z)\end{array}$ to account for the lateral reservoir flow with a constant temperature (see Fig. 1 and Fig. 2).


Fig. 1. Sample Subsurface Temperature Profile around a $\begin{array}{l}h_f\end{array}$ height lateral flow at depth $\begin{array}{l}z_f\end{array}$ with temperature $\begin{array}{l}T_f\end{array}$	Fig. 2. Sample Subsurface Temperature Profile around two lateral flows with temperature $\begin{array}{l}T_{f1}\end{array}$ and $\begin{array}{l}T_{f2}\end{array}$

Outputs

$\begin{array}{l}T_e(t, z)\end{array}$

Subsurface temperature distribution

$\begin{array}{l}t\end{array}$	Time lapse after the temperature step from $\begin{array}{l}T_e(z=0) =0\end{array}$ up to $\begin{array}{l}T_e(z=0) =T_f\end{array}$
$\begin{array}{l}z\end{array}$	Spatial coordinate along the transversal direction to constant temperature $\begin{array}{l}T_e(z)= T_f\end{array}$ plane $\begin{array}{l}z=0\end{array}$
$\begin{array}{l}z_f\end{array}$	TVDss of the top of the lateral flow unit
$\begin{array}{l}h_f\end{array}$	True vertical thickness of the the lateral flow unit
$\begin{array}{l}T_f\end{array}$	Boundary temperature at $\begin{array}{l}z=0\end{array}$
$\begin{array}{l}a_e\end{array}$	Thermal diffusivity of the surroundings
$\begin{array}{l}T_G(z)\end{array}$	Geothermal Temperature Profile

Driving equation

Initial conditions

Boundary conditions

(1)	$\begin{array}{l}\displaystyle \frac{\partial T_e}{\partial t} = a_e^2 \, \Delta T_e = a_e^2 \, \frac{\partial^2 T_e}{\partial z^2}\end{array}$

(2)	$\begin{array}{l}\displaystyle T_e(t=0, z) = T_G(z)\end{array}$

(3)	$\begin{array}{l}\displaystyle T_e(t, z_f \leq z \leq z_f + h_f) = T_f = {\rm const}\end{array}$

(4)	$\begin{array}{l}\displaystyle T_e(t, z \rightarrow \infty) = T_G(z)\end{array}$

(5)	$\begin{array}{l}\displaystyle \mbox{if} \, z < z_f \; \Longrightarrow \;T_e(t,z) = T_f + (T_G(z) - T_f) \cdot \mbox{erf} \left( \frac{z_f-z}{\sqrt{4 a_e t}} \right)\end{array}$

(6)	$\begin{array}{l}\displaystyle \mbox{if} \, z_f \leq z \leq z_f + h_f \; \Longrightarrow \; T_e(t,z) = T_f\end{array}$

(7)	$\begin{array}{l}\displaystyle \mbox{if} \, z > z_f + h_f \; \Longrightarrow \; T_e(t,z) = T_f + (T_G(z) - T_f) \cdot \mbox{erf} \left( \frac{z-z_f-h_f}{\sqrt{4 a_e t}} \right)\end{array}$

where

$\begin{array}{l}\mbox{erf}(x)\end{array}$