Time interval of pressure transition when pressure drop $\begin{array}{l}\delta p\end{array}$ is evolving logarithmically in time:

(1)	$\begin{array}{l}\displaystyle \delta p = p_{wf}(0) - p_{wf}(t) \sim p_{wf}(0) - p_i - \frac{q_t}{4 \pi \sigma} \, \bigg[ - 2S + \gamma - \ln \bigg( \frac{4 \chi t}{r_w^2} \bigg) \bigg]\end{array}$

and hence the pressure log-derivative stays constant:

(2)	$\begin{array}{l}\displaystyle \delta p ' = \frac{d \, \Delta p}{d \, \ln t} = \frac{q_t}{4 \pi \sigma} = \rm const\end{array}$

Since IARF is normally used to define a flow regime during a certain finite period of time, the term "infinite acting" is a misnomer.

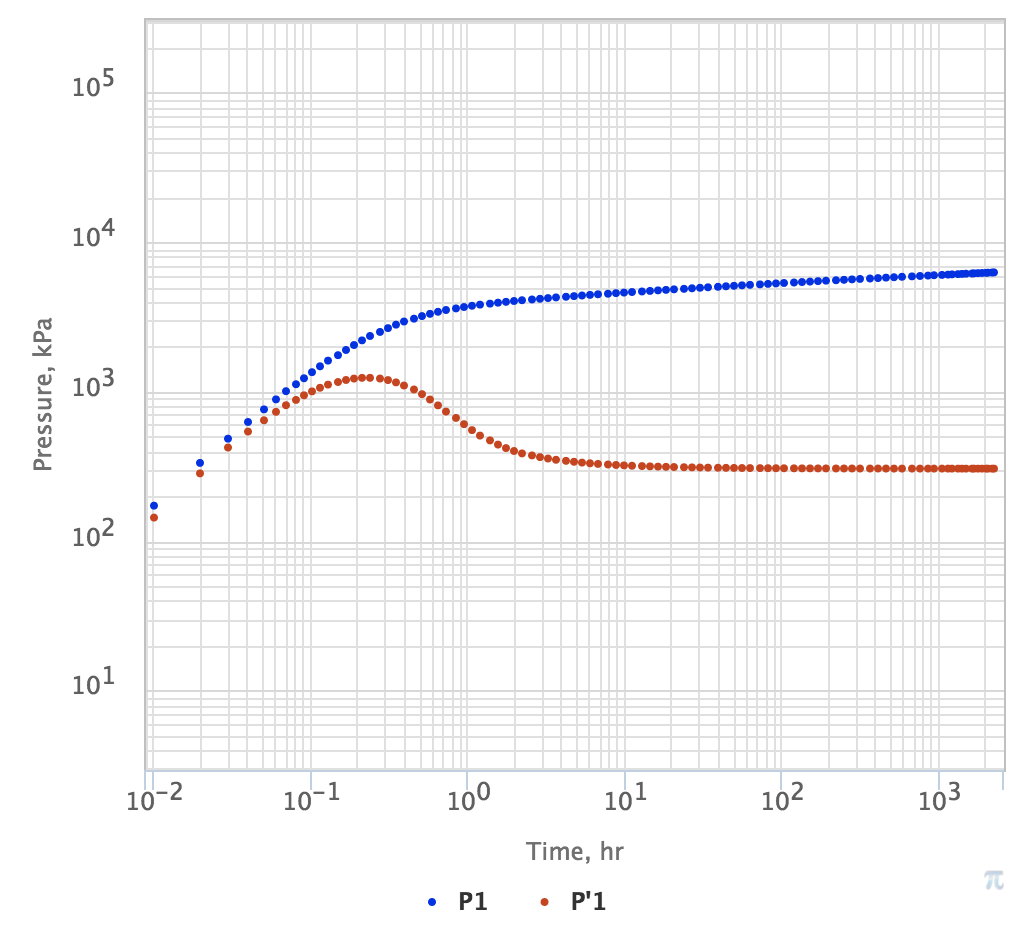
This pressure diffusion regime is native to radial fluid flow in vertical well, homogeneous reservoir and no boundary (see Fig. 1).

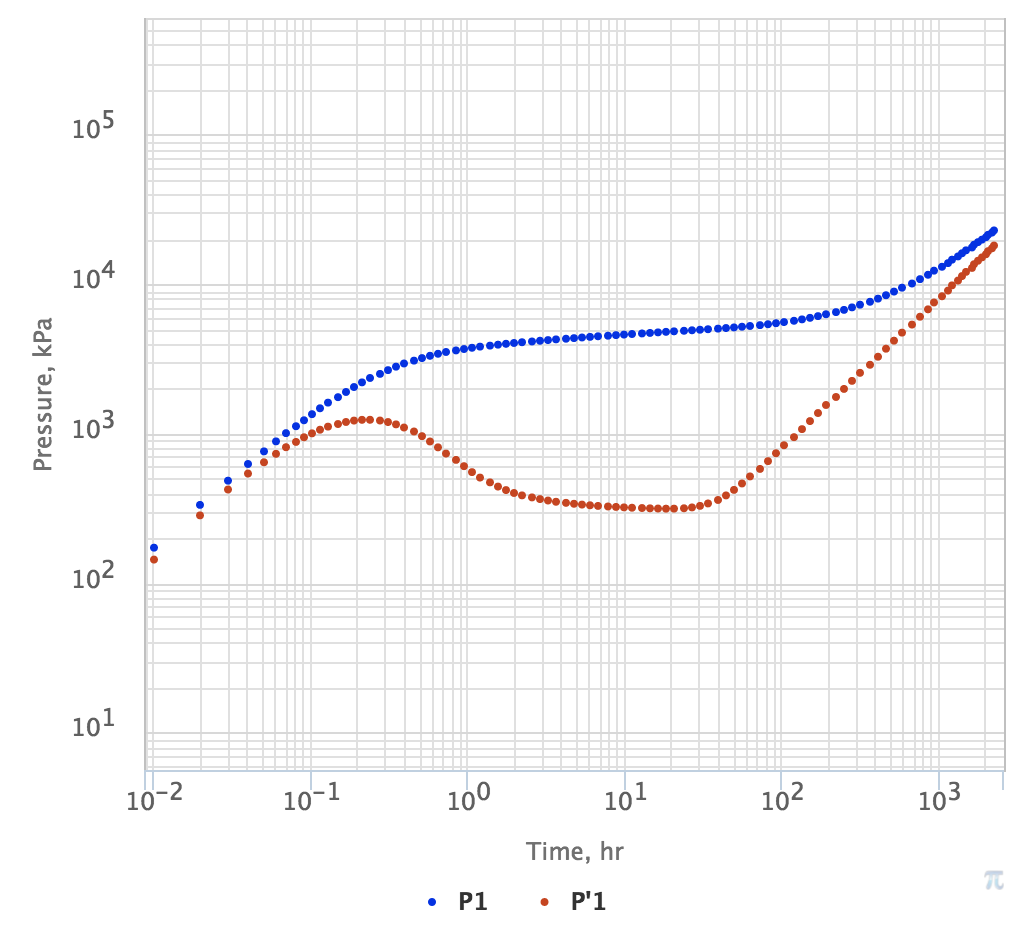
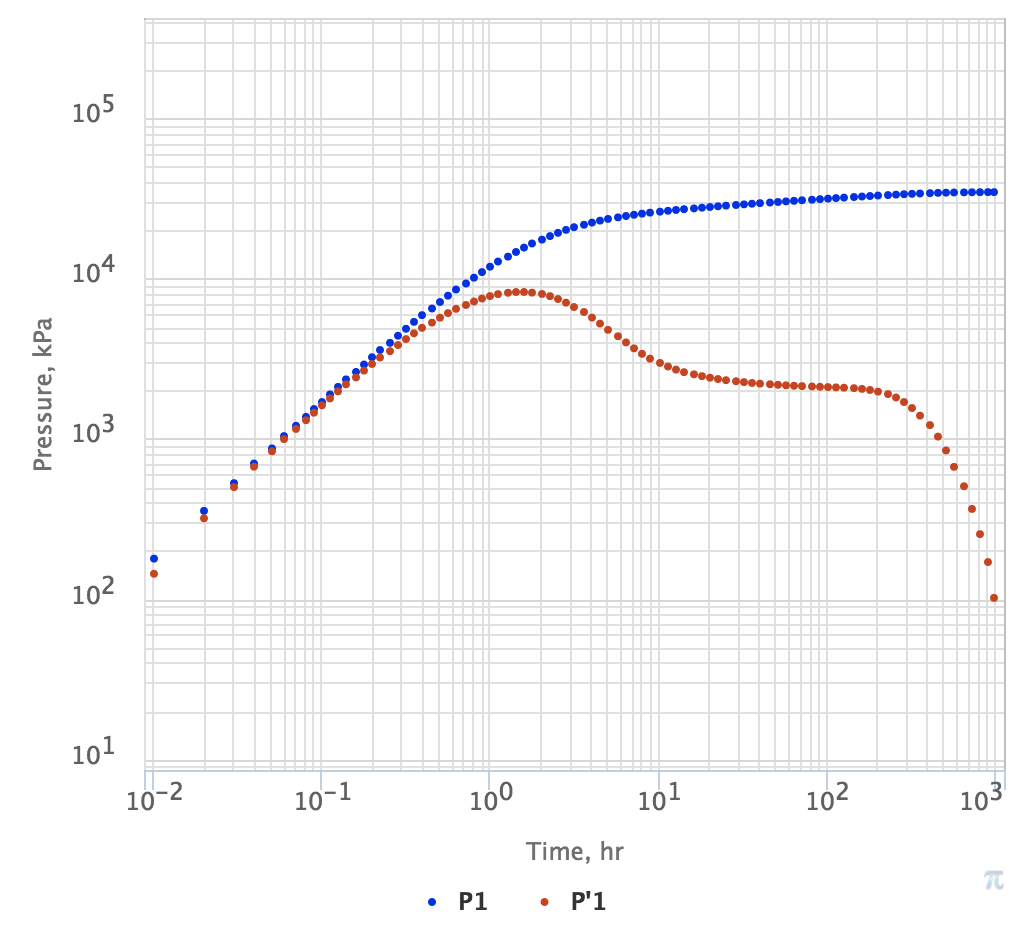
The other popular occurrence of IARF is before PSS (Fig. 2) and SS (Fig. 3).


Fig. 1. PTA Diagnostic Plot with IARF regime developing after 100 hrs	Fig. 2. PTA Diagnostic Plot with IARF regime developing after 100 hrs until PSS at 1,000 hrs	Fig. 3. PTA Diagnostic Plot with IARF regime developing after 100 hrs until SS at 1,000 hrs

Page tree

See Also