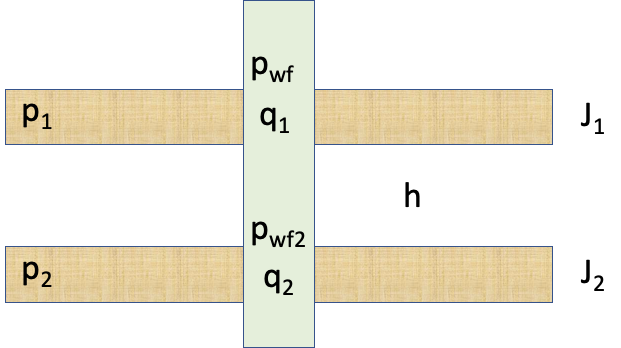
| Fig. 1. Dual-layer well schematic |
|
|
| ||||||
| ||||||||
where
| Well | ||
|---|---|---|
q | total subsurface flowrate of the well | |
J | total well productivity Index | |
p_e | apparent formation pressure of dual-layer formation | |
| Layer #1 | ||
p_{wf} = p_{wf, 1} | bottom-hole pressure at Layer #1 top | |
q_1 | total subsurface flowrate of the Layer #1 | |
p_1 | formation pressure of the Layer #1 | |
J_1 | productivity Index of the Layer #1 | |
| Layer #2 | ||
p_{wf2} = p_{wf} + \delta p_2 | bottom-hole pr4essure at Layer #2 top | |
\delta p_2 | wellbore pressure loss between the tips of two layers | |
q_2 | total subsurface flowrate of the Layer #2 | |
p_2 | formation pressure of the Layer #2 | |
J_2 | productivity Index of the Layer #2 | |
In many practical cases one can safely assume:
| (5) | \delta p_2 = \rho \, g \, h |
where
\rho | wellbore fuid density |
|---|---|
g | gravity constant |
h = TVDSS_1 - TVDSS_2 | true vertical height between k-th layer and reference layer k_{reff} |
The above equations are valid for both producers q>0 and injectors q<0.
See Also
Petroleum Industry / Upstream / Production / Subsurface Production / Subsurface E&P Disciplines / Field Study & Modelling / Production Analysis / Productivity Diagnostics
[ Production Technology / Well Flow Performance ]
[ Formation pressure (Pe) ] [ Multi-layer IPR ]