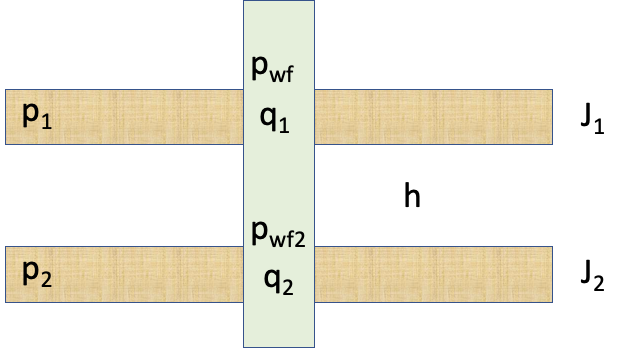
Fig. 1. Dual-layer well schematic

(1)	$\begin{array}{l}\displaystyle q = q_1 + q_2\end{array}$

(2)	$\begin{array}{l}\displaystyle p_{wf} = p_e - q/J\end{array}$

(3)	$\begin{array}{l}\displaystyle J = J_1 + J_2\end{array}$

(4)	$\begin{array}{l}\displaystyle p_e = \frac{J_1 \cdot p_1 + J_2 \cdot (p_2- \delta p_2)}{J_1 + J_2}\end{array}$

where

Well
	$\begin{array}{l}q\end{array}$	total subsurface flowrate of the well
	$\begin{array}{l}J\end{array}$	total well productivity Index
	$\begin{array}{l}p_e\end{array}$	apparent formation pressure of dual-layer formation
Layer #1
	$\begin{array}{l}p_{wf} = p_{wf, 1}\end{array}$	bottom-hole pressure at Layer #1 top
	$\begin{array}{l}q_1\end{array}$	total subsurface flowrate of the Layer #1
	$\begin{array}{l}p_1\end{array}$	formation pressure of the Layer #1
	$\begin{array}{l}J_1\end{array}$	productivity Index of the Layer #1
Layer #2
	$\begin{array}{l}p_{wf2} = p_{wf} + \delta p_2\end{array}$	bottom-hole pr4essure at Layer #2 top
	$\begin{array}{l}\delta p_2\end{array}$	wellbore pressure loss between the tips of two layers
	$\begin{array}{l}q_2\end{array}$	total subsurface flowrate of the Layer #2
	$\begin{array}{l}p_2\end{array}$	formation pressure of the Layer #2
	$\begin{array}{l}J_2\end{array}$	productivity Index of the Layer #2

In many practical cases one can safely assume:

(5)	$\begin{array}{l}\displaystyle \delta p_2 = \rho \, g \, h\end{array}$

where

$\begin{array}{l}\rho\end{array}$	wellbore fuid density
$\begin{array}{l}g\end{array}$	gravity constant
$\begin{array}{l}h = TVDSS_1 - TVDSS_2\end{array}$	true vertical height between $\begin{array}{l}k\end{array}$ -th layer and reference layer $\begin{array}{l}k_{reff}\end{array}$

The above equations are valid for both producers $\begin{array}{l}q>0\end{array}$ and injectors $\begin{array}{l}q< 0\end{array}$ .

Derivation

(6)	$\begin{array}{l}\displaystyle p_{wf, 1} = p_{wf} = p_1 - q_1/J_1\end{array}$

(7)	$\begin{array}{l}\displaystyle p_{wf,2} = p_{wf} + \delta p_2 = p_2 - q_2/J_2\end{array}$

This leads to

(8)	$\begin{array}{l}\displaystyle q_1 = J_1 \cdot (p_1 - p_{wf})\end{array}$

(9)	$\begin{array}{l}\displaystyle q_2 = J_2 \cdot (p_2 - p_{wf,2}) = J_2 \cdot ((p_2-\delta p_2)- p_{wf})\end{array}$

and

(10)	$\begin{array}{l}\displaystyle q = q_1 + q_2 = q_1 = J_1 \cdot (p_1 - p_{wf})+ J_2 \cdot ((p_2-\delta p_2)- p_{wf})\end{array}$

(11)	$\begin{array}{l}\displaystyle q = - (J_1+J_2)\cdot p_{wf} + J_1 \cdot p_1 + J_2 \cdot (p_2-\delta p_2)\end{array}$

or

(12)	$\begin{array}{l}\displaystyle q = J \cdot (p_e - p_{wf}), \ {\rm where} \ J = J_1 + J_2 \ {\rm and} \ p_e = J^{-1} \cdot (J_1 \cdot p_1 + J_2 \cdot (p_2-\delta p_2))\end{array}$

Page tree

See Also