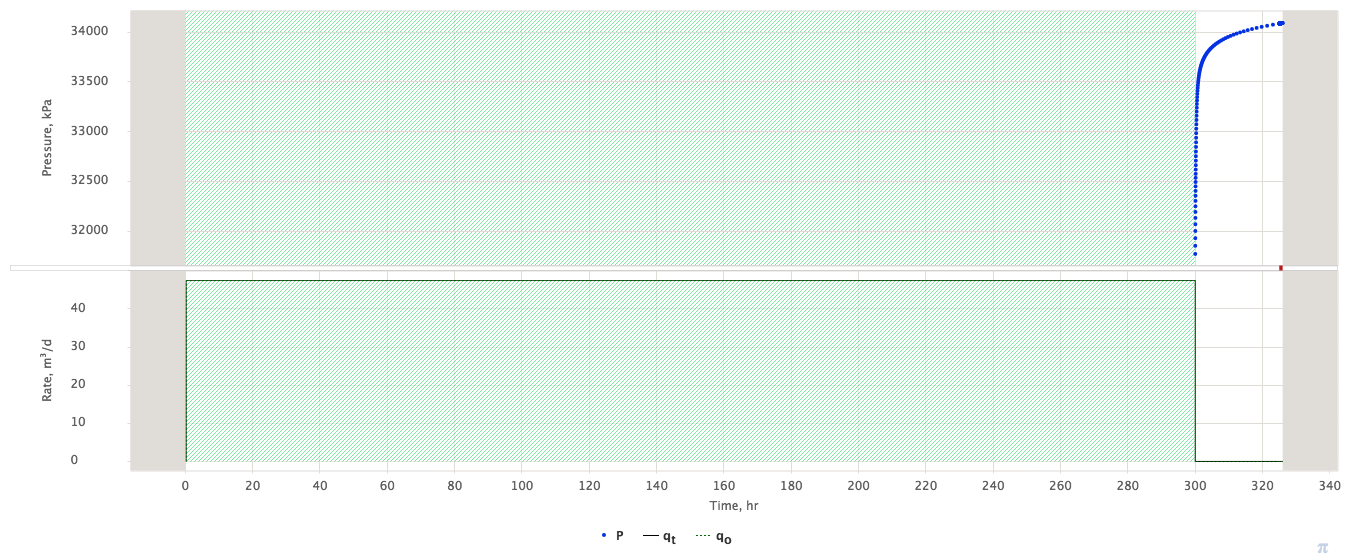
Specific schematic of Pressure Test consisting of long-term shut-in, followed by FLOWING test (Drawdown / Injection) then followed by Build-up / Fall-off (see Fig. 1).

Interpretation of BUS in terms of formation pressure and formation transmissibility under the following (Horner) conditions:

Horner Conditions

both production $\begin{array}{l}T\end{array}$ and shut-in $\begin{array}{l}t\end{array}$ period reach radial flow regime: $\begin{array}{l}T > t_{IARF}\end{array}$ , $\begin{array}{l}t > t_{IARF}\end{array}$

total duration of production and shut-in do not reach the boundary $\begin{array}{l}T+t < t_e\end{array}$

Fig. 1 – Horner Test schematic

In some cases when:

both production $\begin{array}{l}T\end{array}$ and shut-in $\begin{array}{l}\Delta t\end{array}$ period reach radial flow regime: $\begin{array}{l}T > t_{IARF}\end{array}$ , $\begin{array}{l}\Delta t > t_{IARF}\end{array}$

total duration of production and shut-in do not reach the boundary $\begin{array}{l}T+\Delta t < t_e\end{array}$

one can uses Horner model which is a simplified version of BUS interpretation procedure and based on the following pressure diffusion model:

(1)	$\begin{array}{l}\displaystyle p_{wf}(\Delta t) = p_e - \frac{q_t}{4 \pi \sigma} \, \ln \left( 1 + \frac{T}{\Delta t} \right)\end{array}$

The main features of Horner model are:

it provides reliable estimation of formation pressure $\begin{array}{l}p_e\end{array}$ and formation transmissibility $\begin{array}{l}\sigma\end{array}$

it does not require the knowledge of pressure diffusivity $\begin{array}{l}\chi\end{array}$ (unlike the case of a drawdown test)

it does not depend on diffusion model specifics as soon as IARF is developed during the test

it does not provide skin-factor estimation

The formula (1) shows that pressure during the shut-in segment of Honer test is not dependant on skin-factor and pressure diffusivity.

The formation pressure $\begin{array}{l}p_e\end{array}$ and transmissibility $\begin{array}{l}\sigma\end{array}$ are estimated with LSQ regression:

$\begin{array}{l}\displaystyle \left \{ p_{wf} \right \} = p_e - b \, \left \{ \ln \left( 1 + \frac{T}{\Delta t} \right) \right \}\end{array}$

$\begin{array}{l}\displaystyle \sigma = \frac{q_t}{4 \pi b}\end{array}$

Horner model is a good example of how a complicated problem of non-linear regression on three parameters $\begin{array}{l}\{ p_e, \, S, \, \sigma \}\end{array}$ with upfront knowledge of pressure diffusivity may sometimes be simplified to a fast-track linear regression on two parameters without any additional assumptions on reservoir properties.

Page tree

See Also