Horner method @model

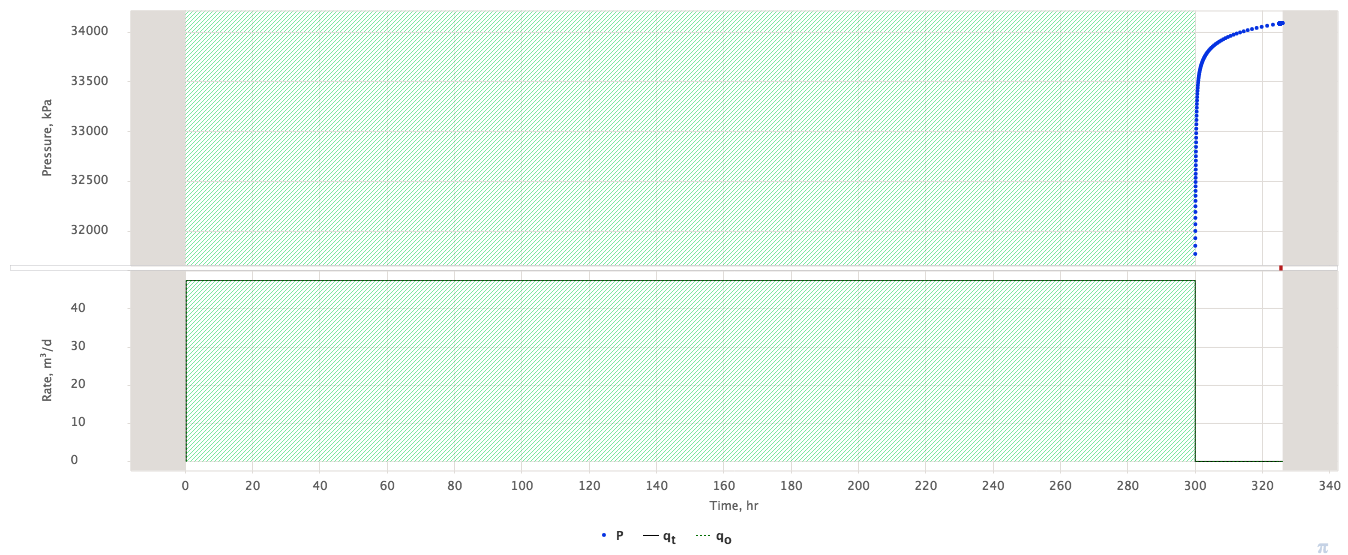
Interpretation of BUS  in terms of formation pressure and formation transmissibility under the following (Horner) conditions:

In some cases when: 

both production  $//<![CDATA[ \begin{array}{l}T\end{array} //]]>$ and shut-in  $//<![CDATA[ \begin{array}{l}\Delta t\end{array} //]]>$ period reach radial flow regime:  $//<![CDATA[ \begin{array}{l}T > t_{IARF}\end{array} //]]>$,  $//<![CDATA[ \begin{array}{l}\Delta t > t_{IARF}\end{array} //]]>$

total duration of production and shut-in do not reach the boundary  $//<![CDATA[ \begin{array}{l}T+\Delta t < t_e\end{array} //]]>$

one can uses Horner model which  is a simplified version of BUS interpretation procedure and based on the following pressure diffusion model:

The main features of Horner model are:

it provides reliable estimation of formation pressure  $//<![CDATA[ \begin{array}{l}p_e\end{array} //]]>$  and formation transmissibility  $//<![CDATA[ \begin{array}{l}\sigma\end{array} //]]>$

it does not require the knowledge of pressure diffusivity  $//<![CDATA[ \begin{array}{l}\chi\end{array} //]]>$ (unlike the case of a drawdown test)

it does not depend on diffusion model specifics as soon as IARF is developed during the test

it does not provide skin-factor estimation

The formula  (1) shows that pressure during the shut-in segment of Honer test is not dependant on skin-factor and pressure diffusivity.

The formation pressure  $//<![CDATA[ \begin{array}{l}p_e\end{array} //]]>$ and transmissibility  $//<![CDATA[ \begin{array}{l}\sigma\end{array} //]]>$ are estimated with LSQ regression:

Horner model is a good example of how a complicated problem of non-linear regression on three parameters   $//<![CDATA[ \begin{array}{l}\{ p_e, \, S, \, \sigma \}\end{array} //]]>$ with upfront knowledge of pressure diffusivity may sometimes be simplified to a  fast-track linear regression on two parameters without any additional assumptions on reservoir properties.

Тест Хорнера относится к частному случаю двухрежимного нестационарного теста (2НТ), при котором скважину после длительной эксплуатации с постоянным дебитом  $//<![CDATA[ \begin{array}{l}q_{t1}\end{array} //]]>$ в течении времени  $//<![CDATA[ \begin{array}{l}T\end{array} //]]>$ отключают и регистрируют динамику забойного давления  $//<![CDATA[ \begin{array}{l}p_{wf}(t)\end{array} //]]>$, где отсечет времени  $//<![CDATA[ \begin{array}{l}t\end{array} //]]>$ ведется с момента остановки скважины. То есть по сути это это 2НТ с  $//<![CDATA[ \begin{array}{l}q_{t2}=0\end{array} //]]>$ (см. рисунок 3).

Из формулы 

Отсюда следует что транзиент давления на остановке не содержит сведения о скин-факторе.

Если однородный пласт полностью вскрыт вертикальной скважиной без трещин и на временах порядка времени наблюдения  $//<![CDATA[ \begin{array}{l}t\end{array} //]]>$ граница не достигается, то диффузия происходит в режиме IARF и  $//<![CDATA[ \begin{array}{l}F(z) \sim \gamma + \ln(-z)\end{array} //]]>$, откуда:

Отсюда видно, что в этом режиме течения влияние пьезопроводности на динамику давления Хорнер-теста полностью отсутствует и с помощью простого  МНК  в координатах  $//<![CDATA[ \begin{array}{l}\{ p_{wf}, \, \ln \frac{t}{t-T} \}\end{array} //]]>$ легко находится пластовое давление на начало теста  $//<![CDATA[ \begin{array}{l}p_e\end{array} //]]>$ и гидропроводность пласта  $//<![CDATA[ \begin{array}{l}\sigma\end{array} //]]>$. 

Хорнер-тест является ярким примером того, как мультирежимный тест позволяет свести сложную задачу анализа транзиента и неоднозначного поиска в трехмерном пространстве  $//<![CDATA[ \begin{array}{l}\{ p_e, \, S, \, \sigma \}\end{array} //]]>$ к последовательности простых прямых вычислительных процедур с однозначным результатом