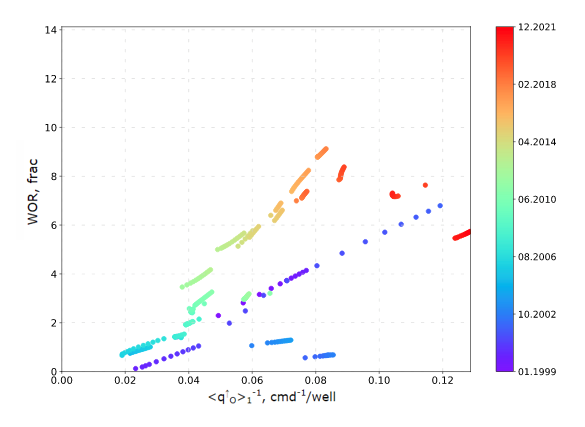
The plot of WOR (along y-axis) against the inverse oil production rate
q_O (along x-axis) (see Fig. 1).
| Fig. 1. WOR (logarithmic vertical axis) vs inverse oil production rate (linear horizontal axis) |
It can be used for express Watercut Diagnostics of thief water production.
The mathematical model of the thief water production from aquifer is based on the following equation:
|
|
|
where
q_W | water production rate | q_O | oil production rate | ||
p^*_1 | J_{1W} | water productivity index of petroleum reservoir | J_{1O} | oil productivity index of petroleum reservoir | |
p^*_2 | formation pressure in aquifer | J_{2W} | water productivity index of aquifer | ||
For the case of aquifer pressure is higher than that of petroleum reservoir: b > 0 \Leftrightarrow p^*_2 > p^*_1
For the case of aquifer pressure is lower than that of petroleum reservoir: b < 0 \Leftrightarrow p^*_2 < p^*_1
In practical applications, the equation (1) is often considered through the weighted average values:
| (4) | \langle WOR \rangle =\frac{\langle q_W \rangle}{\langle q_O \rangle} = a + b \cdot \langle q_O^{-1} \rangle |
where
\langle q_W \rangle, \ \langle q_O \rangle | are weighted average of q_W and q_O |
There are different ways to calculate weighted average of the dynamic variable, for example:
|
|
See Also
Petroleum Industry / Upstream / Production / Subsurface Production / Field Study & Modelling / Production Analysis / Watercut Diagnostics