View Source

We start with reservoir pressure diffusion outside wellbore:

\frac{\partial (\rho \phi)}{\partial t} + \nabla \, ( \rho \, {\bf u}) = 0

\int_{\Sigma_k} \, {\bf u} \,  d {\bf A} = q_k(t)

where

	well-reservoir contact of the -th well
	normal vector of differential area on the well-reservoir contact, pointing inside wellbore

Then use the following equality:

d(\rho \, \phi) = \rho \, d \phi + \phi \, d\rho = \rho \, \phi \, \left( \frac{d \phi }{\phi} +  \frac{d \rho }{\rho}  \right) 
= \rho \, \phi \, \left( \frac{1}{\phi} \frac{d \phi}{dp} \, dp +  \frac{1}{\rho} \frac{d \rho}{dp} \, dp  \right) 
= \rho \, \phi \, (c_{\phi} \, dp + c \, dp) = \rho \, \phi \, c_t \, dp

to arrive at:

\rho \, \phi \, c_t  \cdot \frac{\partial p}{\partial t} + \nabla \, ( \rho \, {\bf u}) = 0

\int_{\Sigma_k} \, {\bf u} \,  d {\bf A} = q_k(t)

where

total compressibility

Let's assume Darcy flow with constant permeability 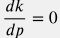and ignore gravity forces:

 {\bf u} = \frac{k}{\mu} \nabla \, p

so that diffusion equation becomes:

\rho \, \phi \, c_t  \cdot \frac{\partial p}{\partial t} + \nabla \, ( k \cdot \frac{\rho}{\mu} \, \nabla  \, p) = 0

\frac{k}{\mu} \cdot \int_{\Sigma_k} \,  {\bf \nabla } \, p \cdot  d {\bf A} = q_k(t)

Let's express the density via Z-factor:

\rho = \frac{M}{RT} \, \frac{p}{Z(p)}

where

	fluid temperature
	molar mass of a fluid
	gas constant

and assuming the fluid temperature 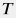does not change over time and space during the modelling period:

 \phi \, c_t \, \mu  \cdot \frac{p}{\mu \, Z} \cdot \frac{\partial p}{\partial t} + \nabla \, ( k \cdot \frac{p}{\mu \, Z} \, \nabla  \, p) = 0

\frac{k}{\mu} \cdot \int_{\Sigma_k} \, {\bf \nabla } \, p \cdot   d {\bf A} = q_k(t)

or

\phi \, c_t \, \mu   \cdot \frac{\partial \Psi}{\partial t} + \nabla \, ( k \cdot \nabla  \, \Psi) = 0

\frac{k}{\mu} \cdot \int_{\Sigma_k} \, {\bf \nabla } \, p \cdot   d {\bf A} = q_k(t)

where

Pseudo-Pressure

In some practical cases the complex can be considered as constant in time which makes a linear differential equation.

But during the early transition times the pressure drop is usually high and the complex can not be considered as constant in time which leads to distortion of pressure transient diagnostics at early times.

In this case one can use Pseudo-Time, calculated by means of the bottom-hole pressure :

\tau(t) = \int_0^t \frac{dt}{\mu (p_{BHP} ) \, c_t (p_{BHP}) } \, , \ \  p_{BHP} = p_{BHP}(t)

to correct early-time transient behaviour which turn equation into:

\phi  \cdot \frac{\partial \Psi}{\partial \tau} + \nabla \, ( k \cdot \nabla  \, \Psi) = 0