1 1DL low-compressibility diffusion in infinite homogeneous reservoir
Рассмотрим плоскопараллельный однородный пласт постоянной толщины 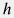 ограниченный в горизонтальной плоскости полосой ширины ограниченный в горизонтальной плоскости полосой ширины 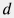 с координатой с координатой 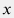 вдоль полосы, которая вскрыта горизонтальной скважиной в точке вдоль полосы, которая вскрыта горизонтальной скважиной в точке  по всей ширине полосы (например, компартмент между двумя параллельными непроницаемыми разломами) и начальным пластовым давлением по всей ширине полосы (например, компартмент между двумя параллельными непроницаемыми разломами) и начальным пластовым давлением 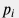 . .
Пусть в момент времени  скважина запускается с дебитом скважина запускается с дебитом 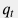 (в пластовых условиях). (в пластовых условиях). Диффузия давления описывается решением уравнения однофазного линейного течения в бесконечном однородном пласте \frac{\partial p}{\partial t} = \chi \, \frac{d^2 p}{dx^2} |
с начальным условием и граничными условиями p(t, x \rightarrow \infty ) = p_i |
\frac{\partial p(t, x )}{\partial x} \bigg|_{x \rightarrow 0} = \frac{q_t}{\sigma \, d} |
где 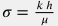 – гидропроводность пласта, – гидропроводность пласта, 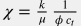 – пьезопроводность пласта, – пьезопроводность пласта, 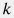 – проницаемость пласта, – проницаемость пласта, 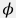 – пористость пласта, – пористость пласта,  – сжимаемость пласта, – сжимаемость пласта, 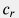 – сжимаемость порового объема трещины, – сжимаемость порового объема трещины, 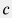 – сжимаемость флюида, насыщающего пласт, – сжимаемость флюида, насыщающего пласт, 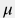 – вязкость флюида, насыщающего пласт. – вязкость флюида, насыщающего пласт.
Решение этого уравнения дается следующим выражением:
p(t,x) = p_i - \frac{q_t}{\sigma \, d} \bigg[ \sqrt{\frac{4 \chi t}{\pi}} \exp \bigg( -\frac{x^2}{4 \chi t} \bigg) - x \, \bigg[ 1- {\rm erf} \bigg(\frac{x}{\sqrt{4 \, \chi \, t}} \bigg) \bigg] \bigg] |
В стволе скважины ( ) динамика давления будет описываться следующей формулой: ) динамика давления будет описываться следующей формулой: p_{wf}(t) = p_i - \frac{q_t}{\sigma \, d} \, \sqrt{\frac{4 \chi t}{\pi}} |
Отсюда следует что динамическая депрессия на пласт растет пропорционально квадратному корню из времени \delta p = p_i - p_{wf}(t) \sim t^{1/2} |
равно как и ее логарифмическая производная t \frac{d (\delta p)}{dt} \sim t^{1/2} |
В лог-лог координатах депрессия и ее лог-производная будут иметь одинаковый слоп 1/2, что является характерным для линейно-одномерной фильтрации.
q |