Motivation

Inputs & Outputs
Physical Model
Mathematical Model
Q^{\downarrow}_{AQ}= B \cdot \int_0^t W_{eD} \left( \frac{(t-\tau)\chi}{r_e^2}, \frac{r_a}{r_e} \right) \dot p(\tau) d\tau |
|
q^{\downarrow}_{AQ}(t)= \frac{dQ^{\downarrow}_{AQ}}{dt} |
|
W_{eD}(t, r)= \int_0^{t} \frac{\partial p_1}{\partial r_D} \bigg|_{r_D = 1} dt_D |
| |
|
| Radial Drive | Linear drive |
|---|
\frac{\partial p_1}{\partial t_D} = \frac{\partial^2 p_1}{\partial r_D^2} + \frac{1}{r_D}\cdot \frac{\partial p_1}{\partial r_D} |
|
|
\frac{\partial p_1}{\partial t_D} = \frac{\partial^2 p_1}{\partial x_D^2} |
| |
|
\frac{\partial p_1(t_D, r_D)}{\partial r_D}
\Bigg|_{r_D=r_{aD}} = 0 |
or p_1(t_D, r_D = \infty) = 0 |
| |
\frac{\partial p_1(t_D, x_D)}{\partial r_D}
\Bigg|_{x_D=x_{aD}} = 0 |
or p_1(t_D, x_D = \infty) = 0 |
|
Transient flow in Radial Composite Reservoir:
\frac{\partial p_a}{\partial t} = \chi \cdot \left[ \frac{\partial^2 p_a}{\partial r^2} + \frac{1}{r}\cdot \frac{\partial p_a}{\partial r} \right] |
| | |
\frac{\partial p_a}{\partial r}
\bigg|_{(t, r=r_a)} = 0 |
|
Consider a pressure convolution:
p_a(t, r) = p(0) + \int_0^t p_1 \left(\frac{(t-\tau) \cdot \chi}{r_e^2}, \frac{r}{r_e} \right) \dot p(\tau) d\tau |
|
\dot p(\tau) = \frac{d p}{d \tau} |
|
One can easily check that  honors the whole set of equations honors the whole set of equations  – – and as such defines a unique solution of the above problem. and as such defines a unique solution of the above problem. Water flowrate within 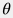 sector angle at interface with oil reservoir will be: sector angle at interface with oil reservoir will be: q^{\downarrow}_{AQ}(t)= \theta \cdot r_e \cdot h \cdot u(t,r_e) |
where  is flow velocity at aquifer contact boundary, which is: is flow velocity at aquifer contact boundary, which is: u(t,r_e) = M \cdot \frac{\partial p_a(t,r)}{\partial r} \bigg|_{r=r_e} |
where  is aquifer mobility. is aquifer mobility. Water flowrate becomes: q^{\downarrow}_{AQ}(t)= \theta \cdot r_e \cdot h \cdot M \cdot \frac{\partial p_a(t,r)}{\partial r} \bigg|_{r=r_e} |
Cumulative water flux: Q^{\downarrow}_{AQ}(t) = \int_0^t q^{\downarrow}_{AQ}(t) dt = \theta \cdot r_e \cdot h \cdot M \cdot \int_0^t \frac{\partial p_a(t,r)}{\partial r} \bigg|_{r=r_e} dt |
Substituting  into into  leads to: leads to: Q^{\downarrow}_{AQ}(t) = \theta \cdot r_e \cdot h \cdot M \cdot \int_0^t d\xi \ \frac{\partial }{\partial r} \left[
\int_0^\xi p_1 \left( \frac{(\xi-\tau)\chi}{r_e^2}, \frac{r}{r_e} \right) \, \dot p(\tau) d\tau
\right]_{r=r_e} |
Q^{\downarrow}_{AQ}(t) = \theta \cdot h \cdot M \cdot \int_0^t d\xi \ \frac{\partial }{\partial r_D} \left[
\int_0^\xi p_1 \left( \frac{(\xi-\tau)\chi}{r_e^2}, r_D \right) \, \dot p(\tau) d\tau
\right]_{r_D=1} |
Q^{\downarrow}_{AQ}(t) = \theta \cdot h \cdot M \cdot \int_0^t d\xi \
\int_0^\xi \frac{\partial p_1}{\partial r_D} \left( \frac{(\xi-\tau)\chi}{r_e^2}, r_D \right) \Bigg|_{r_D=1} \, \dot p(\tau) d\tau
|
The above integral represents the integration over the 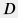 area in area in  plane (see Fig. 1): plane (see Fig. 1): Q^{\downarrow}_{AQ}(t) = \theta \cdot h \cdot M \cdot \iint_D d\xi \ d\tau \, \dot p(\tau)
\frac{\partial p_1}{\partial r_D} \left( \frac{(\xi-\tau)\chi}{r_e^2}, r_D \right) \Bigg|_{r_D=1}
|
| Fig. 1. Illustration of the integration 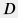 area in area in  plane plane |
Changing the integration order from  to to  leads to: leads to: Q^{\downarrow}_{AQ}(t) = \theta \cdot h \cdot M \cdot \int_0^t d\tau \int_\tau^t d\xi \ \dot p(\tau)
\frac{\partial p_1}{\partial r_D} \left( \frac{(\xi-\tau)\chi}{r_e^2}, r_D \right) \Bigg|_{r_D=1}
=
\theta \cdot h \cdot M \cdot \int_0^t \dot p(\tau) d\tau \int_\tau^t d\xi \
\frac{\partial p_1}{\partial r_D} \left( \frac{(\xi-\tau)\chi}{r_e^2}, r_D \right) \Bigg|_{r_D=1} |
Replacing the variable: \xi = \tau + \frac{r_e^2}{\chi} \cdot t_D \rightarrow t_D = \frac{(\xi-\tau)\chi}{r_e^2} \rightarrow d\xi = \frac{r_e^2}{\chi} \cdot dt_D |
and flux becomes: Q^{\downarrow}_{AQ}(t) = \theta \cdot h \cdot M \cdot \frac{r_e^2}{\chi} \cdot \int_0^t \dot p(\tau) d\tau \int_0^{(t-\tau)\chi/r_e^2}
\frac{\partial p_1( t_D, r_D)}{\partial r_D} \Bigg|_{r_D=1} dt_D = B \cdot \int_0^t \dot p(\tau) d\tau \int_0^{(t-\tau)\chi/r_e^2}
\frac{\partial p_1( t_D, r_D)}{\partial r_D} \Bigg|_{r_D=1} dt_D |
where 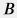 is water influx constant and which leads to is water influx constant and which leads to  and and  . . |
|
Computational Model
Q^{\downarrow}_{AQ}(t)= B \cdot \sum_\alpha W_{eD}
\left( \frac{ (t-\tau_\alpha) \chi}{r_e^2}, \frac{r_a}{r_e} \right)\Delta p_\alpha
= B \cdot W_{eD}
\left( \frac{ (t-\tau_1) \chi}{r_e^2}, \frac{r_a}{r_e} \right)\Delta p_1 +
B \cdot W_{eD}
\left( \frac{ (t-\tau_2) \chi}{r_e^2}, \frac{r_a}{r_e} \right)\Delta p_2
+ ... + B \cdot W_{eD}
\left( \frac{ (t-\tau_N) \chi}{r_e^2}, \frac{r_a}{r_e} \right)\Delta p_N |
|
This computational model is using a discrete convolution (also called superposition in some publications) with time-grid  .
.
In practical exercises with manual or spreadsheet-assisted calculations the time-grid is usually uniform: 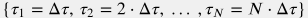 with the time step
with the time step  of a month to ensure the formation pressure does not change much since the previous time step.
of a month to ensure the formation pressure does not change much since the previous time step.
Moving to annual time step may accumulate a substantial mistake if formation pressure has varied substantially in some years.
Scope of Applicability
The benefit of VEH approach is that net pay formation pressure history 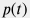 is usually known so that water influx calculation based on aquifer properties
is usually known so that water influx calculation based on aquifer properties 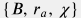 is rather straightforward.
is rather straightforward.
In the past the VEH approach was considered as tedious in calculating superposition during the manual exercises.
In modern computers the convolution is a fast fully-automated procedure and VEH model is considered as a reference in the range of analytical aquifer models.
Although the model is derived for linear and radial flow it also shows a good match for bottom-water drive depletions.
See Also
Petroleum Industry / Upstream / Subsurface E&P Disciplines / Field Study & Modelling / Aquifer Drive / Aquifer Drive Models
Reference
1. van Everdingen, A.F. and Hurst, W. 1949. The Application of the Laplace Transformation to Flow Problems in Reservoirs. Trans., AIME 186, 305.
2. Tarek Ahmed, Paul McKinney, Advanced Reservoir Engineering (eBook ISBN: 9780080498836)
3. Klins, M.A., Bouchard, A.J., and Cable, C.L. 1988. A Polynomial Approach to the van Everdingen-Hurst Dimensionless Variables for Water Encroachment. SPE Res Eng 3 (1): 320-326. SPE-15433-PA. http://dx.doi.org/10.2118/15433-PA
.
with the time step
of a month to ensure the formation pressure does not change much since the previous time step.
is usually known so that water influx calculation based on aquifer properties
is rather straightforward.