Transient flow in Radial Composite Reservoir:
\frac{\partial p_a}{\partial t} = \chi \cdot \left[ \frac{\partial^2 p_a}{\partial r^2} + \frac{1}{r}\cdot \frac{\partial p_a}{\partial r} \right] |
| | |
\frac{\partial p_a}{\partial r}
\bigg|_{(t, r=r_a)} = 0 |
|
Consider a pressure convolution:
p_a(t, r) = p(0) + \int_0^t p_1 \left(\frac{(t-\tau) \cdot \chi_a}{r_e^2}, \frac{r}{r_e} \right) \dot p(\tau) d\tau |
|
\dot p(\tau) = \frac{d p}{d \tau} |
|
One can easily check that  honors the whole set of equations  – and as such defines a unique solution of the above problem. Water flowrate within 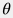 sector angle at interface with oil reservoir will be: q^{\downarrow}_{AQ}(t)= \theta \cdot r_e \cdot h_a \cdot u(t,r_e) |
where  is flow velocity at aquifer contact boundary, which is: u(t,r_e) = M_a \cdot \frac{\partial p_a(t,r)}{\partial r} \bigg|_{r=r_e} |
where  is aquifer mobility. Water flowrate becomes: q^{\downarrow}_{AQ}(t)= \theta \cdot r_e \cdot h_a \cdot M_a \cdot \frac{\partial p_a(t,r)}{\partial r} \bigg|_{r=r_e} |
Cumulative water flux: Q^{\downarrow}_{AQ}(t) = \int_0^t q^{\downarrow}_{AQ}(t) dt = \theta \cdot r_e \cdot h_a \cdot M_a \cdot \int_0^t \frac{\partial p_a(t,r)}{\partial r} \bigg|_{r=r_e} dt |
Q^{\downarrow}_{AQ}(t) = \theta \cdot r_e \cdot h_a \cdot M_a \cdot \int_0^t \frac{1}{r_e} \frac{\partial p_a(t \cdot \frac{r_e^2}{\chi_a},R_E \cdot r_D)}{\partial r_D} \bigg|_{r=r_e} \frac{r_e^2}{\chi_a} dt_D = \theta r_e^2 \cdot h_a \cdot c_t \phi \cdot \int_0^t \frac{\partial p_a(t \cdot \frac{r_e^2}{\chi_a},r_e \cdot r_D)}{\partial r_D} \bigg|_{r_D=1} dt_D = B \cdot \int_0^t \frac{\partial p_a(t \cdot \frac{r_e^2}{\chi_a},r_e \cdot r_D)}{\partial r_D} \bigg|_{r_D=1} dt_D |
Substituting into  leads to: Q^{\downarrow}_{AQ}(t) = \theta \cdot r_e^2 \cdot h_a \cdot c_t \cdot \phi \cdot
\int_0^t \left[ int_0^{(t-\tau)r_e^2/\chi_a} \frac{\partial p_a(t \cdot \frac{r_e^2}{\chi_a},r_e \cdot r_D)}{\partial r_D} \bigg|_{r_D=1} \right] dt_D |
| 