В процессе эксплуатации нагнетательной скважины движение флюида вдоль ствола 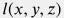 происходит в стационарном режиме, при этом профиль скорости потока происходит в стационарном режиме, при этом профиль скорости потока 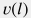 и давления и давления 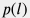 удовлетворяют удовлетворяют условию баланса массы движущегося потока: A(l) \, \rho(l) \, v(l) = \rm const |
и баланса сил действующих на единицу объема флюида в стволе скважины: \frac{dp}{dl} = \rho \, g \, \cos \theta - \rho \, v \, \frac{dv}{dl} - \frac{ f \, \rho \, v^2 \, }{2 d} |
где | длина ствола скважины, отсчитываемая вниз от поверхности | | | профиль плотности воды | | Inclinational Deviation | | профиль диаметра скважины, вдоль которого идет поток | | профиль поперечного сечения ствола скважины  | | профиль коэффициента трения Дарси | | ускорение свободного падения ( = 9.87 м2/сек ) | |
|
Эти замкнутая система уравнений для стационарного распределения давления и скорости потока вдоль трубы.
Для несжимаемой жидкости  в отсутствии трения в отсутствии трения 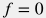 уравнение уравнение  принимает вид: принимает вид: \frac{dp}{dl} = \rho \, g \, \cos \theta - \rho \, v \, \frac{dv}{dl} |
и может быть явно проинтегрировано: p(l) - \rho \, g \, l \, \cos \theta + \frac{1}{2} \rho \, v^2 = \rm const |
и называется уравнением Бернулли.
Если дебит скважины на устье составляет 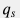 , а плотность воды на устье , а плотность воды на устье 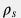 , то уравнение , то уравнение  можно записать в следующем виде: можно записать в следующем виде: A \, \rho \, v = \rho_s \, q_s |
откуда можно выразить явно профиль скорости потока по стволу: v(l) = \frac{\rho_s \, q_s}{\rho(p) \, A(l)} |
Подставляя  в в  получим уравнение на профиль давления вдоль ствола: получим уравнение на профиль давления вдоль ствола: \frac{dp}{dl} = \rho \, g \, \cos \theta - \frac{\rho_s^2 \, q_s^2}{A} \frac{d}{dl} \bigg( \frac{1}{A \, \rho} \bigg) - \frac{\rho_s^2 \, q_s^2 }{2 A^2 d} \frac{f}{\rho} |
Далее учтем, что угол наклона к горизонту 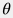 может быть выражен через абсолютные отметки глубин может быть выражен через абсолютные отметки глубин 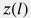 вдоль траектории скважины вдоль траектории скважины 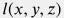 : : \cos \theta = \frac{dz}{dl} |
и уравнение для давление примет вид: \frac{dp}{dl} = \rho \, g \, \frac{dz}{dl} - \frac{\rho_s^2 \, q_s^2}{A} \frac{d}{dl} \bigg( \frac{1}{A \, \rho} \bigg) - \frac{\rho_s^2 \, q_s^2 }{2 A^2 d} \frac{f}{\rho} |
Диаметр труб, вдоль которых идет движение воды, остается постоянным на долгом протяжении и меняется редко (например, километр НКТ и потов выход потока в колонну), и это позволяет решать задачу нахождения профиля давления на кусках постоянного диаметра  и уравнение может быть переписано следующим образом: и уравнение может быть переписано следующим образом: \frac{dp}{dl} = \rho \, g \, \frac{dz}{dl} - \frac{\rho_s^2 \, q_s^2}{A^2} \frac{d}{dl} \bigg( \frac{1}{\rho} \bigg) - \frac{\rho_s^2 \, q_s^2 }{2 A^2 d} \frac{f}{\rho} |
Процесс движения воды вдоль трубы происходит в состоянии термодинамического равновесия и плотность воды является функцией только давления 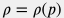 и, следовательно: и, следовательно: \frac{d}{dl} \bigg( \frac{1}{\rho} \bigg) = -\frac{1}{\rho^2} \frac{d \rho}{ dl}
= - \frac{1}{\rho^2}\frac{d \rho}{dp} \frac{dp}{ dl}
=- \frac{c}{\rho} \frac{dp}{ dl} |
где 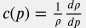 – сжимаемость воды и уравнение профиля давления принимает вид: – сжимаемость воды и уравнение профиля давления принимает вид: \left( 1 - \frac{c(p) \, \rho_s^2 \, q_s^2}{\rho \, A^2} \right ) \frac{dp}{dl} = \rho(p) \, g \, \frac{dz}{dl} - \frac{\rho_s^2 \, q_s^2 }{2 A^2 d} \frac{f(p)}{\rho(p)} |
Функция 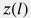 определяется траекторией скважины. определяется траекторией скважины.
Cжимаемость 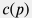 и плотность и плотность 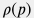 воды слабо зависят от вариации давления вдоль ствола. воды слабо зависят от вариации давления вдоль ствола. Как будет показано ниже коэффициент трения 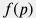 тоже слабо зависит от вариации давления и, следовательно, уравнение тоже слабо зависит от вариации давления и, следовательно, уравнение  представляет собой обыкновенное дифференциальное уравнение первого порядка на функцию представляет собой обыкновенное дифференциальное уравнение первого порядка на функцию 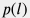 со слабой нелинейностью. со слабой нелинейностью.
|
and
into
: