Профиль давления
В процессе эксплуатации нагнетательной скважины движение флюида вдоль ствола 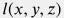 происходит в стационарном режиме, при этом профиль скорости потока происходит в стационарном режиме, при этом профиль скорости потока 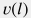 и давления и давления 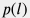 удовлетворяют удовлетворяют условию баланса массы движущегося потока: A(l) \, \rho(l) \, v(l) = \rm const |
и баланса сил действующих на единицу объема флюида в стволе скважины: \frac{dp}{dl} = \rho \, g \, \sin \theta - \rho \, v \, \frac{dv}{dl} - \frac{ f \, \rho \, v^2 \, }{2 d} |
где | длина ствола скважины, отсчитываемая вниз от поверхности | | | профиль плотности воды | | профиль угла наклона скважины к горизонту | | профиль диаметра скважины, вдоль которого идет поток | | профиль поперечного сечения ствола скважины  | | профиль коэффициента трения Дарси | | ускорение свободного падения ( = 9.87 м2/сек ) | |
|
Эти замкнутая система уравнений для стационарного распределения давления и скорости потока вдоль трубы.
Уравнение  часто в литературе записывают как разложение изменения давление вдоль ствола скважины на компоненты: часто в литературе записывают как разложение изменения давление вдоль ствола скважины на компоненты: \frac{dp}{dl} = \bigg( \frac{dp}{dl} \bigg)_g + \bigg( \frac{dp}{dl} \bigg)_v + \bigg( \frac{dp}{dl} \bigg)_f |
где
\bigg( \frac{dp}{dl} \bigg)_g = \rho \, g \, \sin \theta, |
|
гидростатическая компонента вариации давления, формируемая гравитационными силами
- в случае движения флюида вниз она имеет положительный знак и приводит к приросту давления
- в случае движения жидкости наверх эта компонента имеет отрицательный знак и приводит
к потере давления в процессе подъема жидкости
|
\bigg( \frac{dp}{dl} \bigg)_v = - \rho \, v \, \frac{dv}{dl}, |
|
кинетическая компонента вариация давления, формируемая вариацией скорости потока 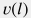 вдоль ствола скважины, которая вызвана сжатием-расжатием флюида и изменением диаметра труб вдоль ствола скважины, которая вызвана сжатием-расжатием флюида и изменением диаметра труб - в случае падения скорости потока в направлении движения она имеет положительный знак и приводит к приросту давления
- в случае роста скорости потока в направлении движения она имеет отрицательный знак и приводит к потере давления
|
\bigg( \frac{dp}{dl} \bigg)_f = - \frac{ f \, \rho v^2}{2 d}, |
|
фрикционная компонента вариации давления, формируемая трением флюида со стенкой скважины она всегда имеет отрциательный знак и приводит к потере давления вдоль направления движения потока |
Для несжимаемой жидкости  в отсутствии трения в отсутствии трения 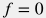 уравнение уравнение  принимает вид: принимает вид: \frac{dp}{dl} = \rho \, g \, \sin \theta - \rho \, v \, \frac{dv}{dl} |
и может быть явно проинтегрировано: p(l) - \rho \, g \, l \, \sin \theta + \frac{1}{2} \rho \, v^2 = \rm const |
и называется уравнением Бернулли.
Уравнение неразрывности одномерного потока с линейной плотностью 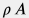 массы: массы: \frac{\partial (\rho A)}{\partial t} + \frac{\partial}{\partial l} \big( A \, \rho \, v \big) = 0 |
для стационарного режима течения принимает вид: \frac{\partial (\rho A)}{\partial t} = - \frac{\partial}{\partial l} \big( A \, \rho \, v \big) = 0 |
откуда и следует формула  . .
Для вывода уравнения  заметим, что на бесконечно малый элемент объема жидкости заметим, что на бесконечно малый элемент объема жидкости 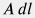 массой массой 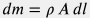 действуют четыре сил: действуют четыре сил: 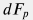 – сила гидравлического напора, вызванная разностью давлений на торцах элемента, – сила гидравлического напора, вызванная разностью давлений на торцах элемента,
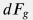 – сила гравитации, – сила гравитации,
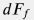 – сила трения со стенками трубы, – сила трения со стенками трубы,
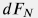 – номральная реакция опоры стенок трубы. – номральная реакция опоры стенок трубы.
Рассмотрим стационарное (то есть установившееся во времени) течение потока по трубе.
Движение поперек трубы отсуствует и, следовательно, сумма проекций всех сил на трансверсальное направление 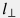 к трубе должно равняться нулю: к трубе должно равняться нулю: dF_p \bigg |_{l_{\perp}} + dF_g \bigg |_{l_{\perp}} + dF_f \bigg |_{l_{\perp}}+ dF_N \bigg |_{l_{\perp}} =0 |
и выполняется автоматически, при наличии достаточного запаса прочности трубы 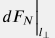 . .
Уравнение движения флюида вдоль оси трубы 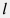 имеет вид: имеет вид:
dF_p \bigg |_l + dF_g \bigg |_l + dF_f \bigg |_l+ dF_N \bigg |_l = \frac{d I}{dt}\bigg |_l |
где 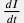 представляет собой изменение импульса представляет собой изменение импульса 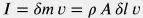 элементарного объема флюида под действием внешних сил. элементарного объема флюида под действием внешних сил.
Изменение импульса c учетом стационарности скорости потока 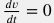 и сохранения массы и сохранения массы 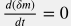 имеет вид: имеет вид: 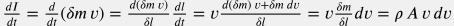 . . Сила, формируемая гидравлическим напором 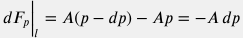 . . Проекция гравитационной силы 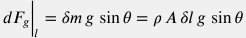 . . Сила трения со стенками трубы дается феноменологическим уравнением Дарси-Вейсбаха: 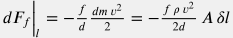 . . Аксиальная компонента реакции опоры труб по определению отсутствует 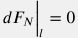 . . Подставляя вышеприведенные выражения в уравнение  получим: получим:
- A dp + \rho \, A\, \delta l \, g \, \sin \theta - \frac{f \, \rho \, v^2}{2 d} \, A \, \delta l = \rho \, A \, v \, dv
|
Разделив уравнение на бесконечно малый объем элемента 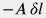 получим получим  . . |
|
Если дебит скважины на устье составляет 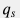 , а плотность воды на устье , а плотность воды на устье 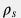 , то уравнение , то уравнение  можно записать в следующем виде: можно записать в следующем виде: A \, \rho \, v = \rho_s \, q_s |
откуда можно выразить явно профиль скорости потока по стволу: v(l) = \frac{\rho_s \, q_s}{\rho(p) \, A(l)} |
Подставляя  в в  получим уравнение на профиль давления вдоль ствола: получим уравнение на профиль давления вдоль ствола: \frac{dp}{dl} = \rho \, g \, \sin \theta - \frac{\rho_s^2 \, q_s^2}{A} \frac{d}{dl} \bigg( \frac{1}{A \, \rho} \bigg) - \frac{\rho_s^2 \, q_s^2 }{2 A^2 d} \frac{f}{\rho} |
Далее учтем, что угол наклона к горизонту 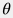 может быть выражен через абсолютные отметки глубин может быть выражен через абсолютные отметки глубин 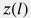 вдоль траектории скважины вдоль траектории скважины 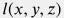 : : \sin \theta = \frac{dz}{dl} |
и уравнение для давление примет вид: \frac{dp}{dl} = \rho \, g \, \frac{dz}{dl} - \frac{\rho_s^2 \, q_s^2}{A} \frac{d}{dl} \bigg( \frac{1}{A \, \rho} \bigg) - \frac{\rho_s^2 \, q_s^2 }{2 A^2 d} \frac{f}{\rho} |
Диаметр труб, вдоль которых идет движение воды, остается постоянным на долгом протяжении и меняется редко (например, километр НКТ и потов выход потока в колонну), и это позволяет решать задачу нахождения профиля давления на кусках постоянного диаметра  и уравнение может быть переписано следующим образом: и уравнение может быть переписано следующим образом: \frac{dp}{dl} = \rho \, g \, \frac{dz}{dl} - \frac{\rho_s^2 \, q_s^2}{A^2} \frac{d}{dl} \bigg( \frac{1}{\rho} \bigg) - \frac{\rho_s^2 \, q_s^2 }{2 A^2 d} \frac{f}{\rho} |
Процесс движения воды вдоль трубы происходит в состоянии термодинамического равновесия и плотность воды является функцией только давления 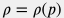 и, следовательно: и, следовательно: \frac{d}{dl} \bigg( \frac{1}{\rho} \bigg) = -\frac{1}{\rho^2} \frac{d \rho}{ dl}
= - \frac{1}{\rho^2}\frac{d \rho}{dp} \frac{dp}{ dl}
=- \frac{c}{\rho} \frac{dp}{ dl} |
где 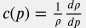 – сжимаемость воды и уравнение профиля давления принимает вид: – сжимаемость воды и уравнение профиля давления принимает вид: \bigg( 1 - \frac{c(p) \, \rho_s^2 \, q_s^2}{A^2} \bigg ) \frac{dp}{dl} = \rho(p) \, g \, \frac{dz}{dl} - \frac{\rho_s^2 \, q_s^2 }{2 A^2 d} \frac{f(p)}{\rho(p)} |
Функция 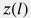 определяется траекторией скважины. определяется траекторией скважины.
Cжимаемость 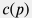 и плотность и плотность 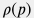 воды слабо зависят от вариации давления вдоль ствола. воды слабо зависят от вариации давления вдоль ствола. Как будет показано ниже коэффициент трения 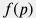 тоже слабо зависит от вариации давления и, следовательно, уравнение тоже слабо зависит от вариации давления и, следовательно, уравнение  представляет собой обыкновенное дифференциальное уравнение первого порядка на функцию представляет собой обыкновенное дифференциальное уравнение первого порядка на функцию 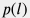 со слабой нелинейностью. со слабой нелинейностью.
Если предположить постоянство коэффициента трения 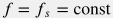 и несжимаемость флюида и несжимаемость флюида 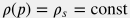 , то уравнение , то уравнение  можно явно проинтегрировать: можно явно проинтегрировать: p(l) = p_s + \rho \, g \, z(l) - \frac{\rho_s \, q_s^2 }{2 A^2 d} \, f_s \, l |
Pressure gradient will be: \frac{dp}{dl} = \cos \theta(l) - \frac{\rho_s \, q_s^2 }{2 A^2 d} \, f_s |
where 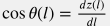 The first term defines the hydrostatic column of static fluid while the last term defines the friction losses under fluid movement: \frac{dp}{dl} \Bigg|_{loss} = \frac{\rho_s \, q_s^2 }{2 A^2 d} \, f_s |
В калькуляторе Well Flow Performance Calculator можно оценить величину потерь на трения для различных сценариев диаметров труб и дебитов скважин. |
along-hole ( see Darcy friction factor in water producing/injecting wells ).