@wikipedia

Darcy friction factor 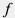depends on Reynolds number and a shape and roughness 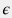of inner pipe walls:

f = f({\rm Re}, \epsilon)

For a smooth (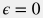) tubular pipeline Darcy friction factor 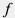can be estimated from various empirical correlations :

f = 64 \, \rm Re^{-1}

Laminar fluid flow

no universal correlations due to a high flow instability

Laminar-turbulent transition fluid flow

f = 0.32 \, \rm Re^{-0.25}

Turbulent fluid flow

f = 0.184 \, \rm Re^{-0.2}

Strong-turbulent fluid flow

where

	Reynolds number
	Inner diameter of a pipe
	dynamic fluid viscosity as function of pressure and temperature along the pipe

For non-smooth pipelines the Darcy friction factor 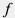can be estimated from empirical Colebrook–White correlation which works for non-laminar flow:

\frac{1}{\sqrt{f}} = -2 \, \log \Bigg( \frac{\epsilon}{3.7 \, d}  + \frac{2.51}{{\rm Re} \sqrt{f}} \Bigg)

Typical surface roughness of a factory steel pipelines is 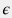= 0.05 mm which may increase significantly under mineral sedimentation or erosive impact of the flowing fluids.

See Surface roughness for more data on typical values for various materials and processing conditions.

Interpolated full-range model

The most popular full-range model of Darcy friction factor is:

\begin{cases}
f = 64/\mbox{Re} & \forall &  \mbox{Re}<2,100
\\f = 0.03048 + k \cdot ( \mbox{Re} -2,100) &  \forall & 2,100 < \mbox{Re}<4,000 
\\f = f_{CW}( \mbox{Re}, \, \epsilon) & \forall & \mbox{Re}>4,000
\end{cases}

where

	Colebrook–White correlation
	interpolation multiplier between laminar and turbulent flow regimes

Bellos full-range model

f = \frac{64}{\rm Re} \cdot \Phi

\Phi = \left( \frac{{\rm Re}}{64} \right)^{1-a}
\cdot \left( 0.75 \cdot \ln \frac{{\rm Re}}{5.37} \right)^{-2 \,(1-a)\,b}
\cdot \left( 0.83 \cdot \ln \frac{3.41}{\epsilon/d} \right)^{-2 \,(1-a)\,(1-b)}

a = \left[ 1+ \left( \frac{{\rm Re}}{2712} \right)^{8.4} \right]^{-1}

b = \left[ 1+ \left( \frac{{\rm Re} \cdot \epsilon/d}{150} \right)^{1.8} \right]^{-1}

Cheng full-range model

f = \frac{64}{\rm Re} \cdot \Phi

\Phi = \left( \frac{{\rm Re}}{64} \right)^{1-a}
\cdot \left( 1.8 \cdot \ln \frac{{\rm Re}}{6.8} \right)^{-2 \,(1-a)\,b}
\cdot \left( 2.0 \cdot \ln \frac{3.7}{\epsilon/d} \right)^{-2 \,(1-a)\,(1-b)}

a = \left[ 1+ \left( \frac{{\rm Re}}{2720} \right)^9 \right]^{-1}

b = \left[ 1+ \left( \frac{{\rm Re} \cdot \epsilon/d}{160} \right)^2 \right]^{-1}

Churchill full-range model

f = \frac{64}{\rm Re} \cdot \Phi

\Phi = \left[ 1+ \frac{\left(\rm Re / 8 \right)^{12} }{ \left( \Theta_1 + \Theta_2 \right)^{1.5} }  \right]^{1/12}

\Theta_1 = \left[  2.457 \, \ln \left(  \left( \frac{7}{\rm Re} \right)^{0.9}  + 0.27 \, \frac{\epsilon}{d}  \right)   \right]^{16}

\Theta_2 = \left(  \frac{37530}{\rm Re} \right)^{16}

Reference

Moody’s Friction Factor Calculator @ gmallya.com