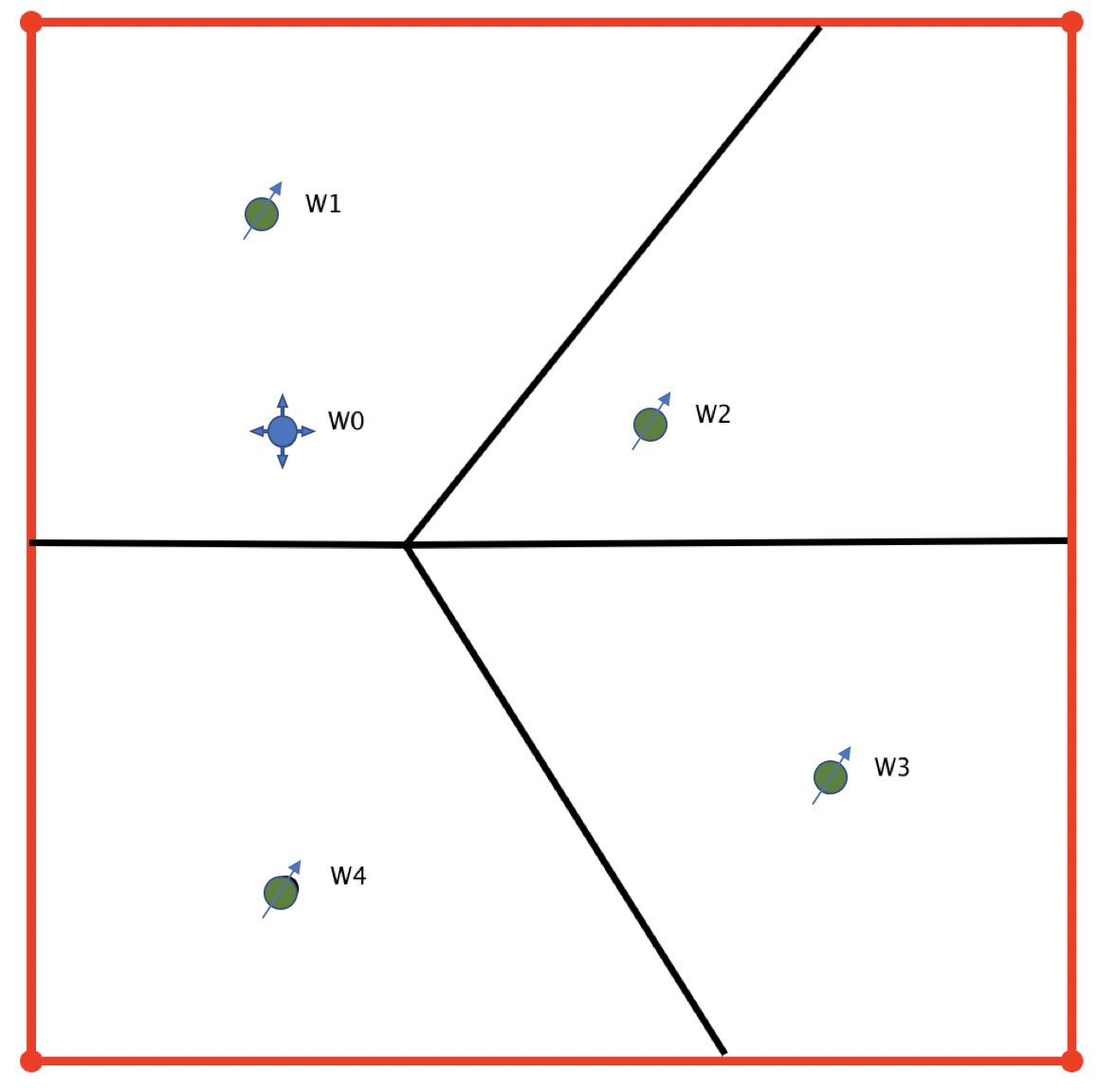
Consider a well-reservoir system (Fig. 1) consisting of:

producing well W₁ with total sandface flowrate $\begin{array}{l}q_1(t)>0\end{array}$ and BHP $\begin{array}{l}p_1(t)>0\end{array}$ , draining the reservoir volume $\begin{array}{l}V_{\phi, 1}\end{array}$
water injecting well W₀ with total sandface flowrate $\begin{array}{l}q_0(t) < 0\end{array}$ , supporting pressure in reservoir volume $\begin{array}{l}V_{\phi, 0}\end{array}$

The injection drainage volume $\begin{array}{l}V_{\phi, 0}\end{array}$ includes the drainage volume $\begin{array}{l}V_{\phi, 1}\end{array}$ of producer W₁ and may be equal to it $\begin{array}{l}V_{\phi, 0} = V_{\phi, 1}\end{array}$ or may be bigger $\begin{array}{l}V_{\phi, 0} > V_{\phi, 1}\end{array}$ in case injector W₀ supports other producers {W₁ .. W_N}: $\begin{array}{l}V_{\phi, 0} = \sum_{k=1}^N V_{\phi, k}\end{array}$ .

Fig. 1. Location map of injector-producer pairing with 4 producers {W₁, W₂, W₃, W₄} and one injector W₀.

Case #1 – Constant flowrate production: $\begin{array}{l}q_1 = \rm const >0\end{array}$

The bottom-hole pressure response $\begin{array}{l}\delta p_1\end{array}$ in producer W₁ to the flowrate variation $\begin{array}{l}\delta q_0\end{array}$ in injector W₀:

(1)	$\begin{array}{l}\displaystyle \delta p_1 = - p_{u,\rm 21}(t) \cdot \delta q_0\end{array}$

where

$\begin{array}{l}t\end{array}$	time since the water injection rate has changed by the $\begin{array}{l}\delta q_0\end{array}$ value.
$\begin{array}{l}p_{u,\rm 01}(t)\end{array}$	cross-well pressure transient response in producer W₁ to the unit-rate production in injector W₀

Derivation

Consider a pressure convolution equation for the BHP in producer W₁with constant flowrate production at producer W₁ $\begin{array}{l}q_1 = \rm const\end{array}$ and varying injection rate at injector W₂ $\begin{array}{l}q_2(t)\end{array}$ :

(2)	$\begin{array}{l}\displaystyle p_1(t) = p_i - \int_0^t p_{u,\rm 11}(t-\tau) dq_1(\tau) - \int_0^t p_{u,\rm 01}(t-\tau) dq_0(\tau) = p_i - \int_0^t p_{u,\rm 01}(t-\tau) dq_0(\tau)\end{array}$

Consider a step-change in injector's W₀ flowrate $\begin{array}{l}\delta q_0\end{array}$ at zero time $\begin{array}{l}\tau = 0\end{array}$ , which can be writen as

(3)	$\begin{array}{l}\displaystyle q_0(\tau) = \delta q_0 \cdot H(\tau)\end{array}$

where $\begin{array}{l}H(\tau)\end{array}$ is Heaviside step function:

(4)	$\begin{array}{l}H(\tau) = \begin{cases} 0, & \tau < 0 \\ 1, &\tau \geq 0\end{cases}\end{array}$

The differential $\begin{array}{l}dq_0\end{array}$ then can be written as:

(5)	$\begin{array}{l}\displaystyle d q_0(\tau) = q_0'(\tau) d\tau = \delta q_0 \cdot H'(\tau) \, d\tau = \delta q_0 \cdot \delta(\tau) \, d\tau\end{array}$

The responding pressure variation $\begin{array}{l}\delta p_1\end{array}$ in producer W₁will be:

(6)	$\begin{array}{l}\displaystyle \delta p_1(t) = p_1(t)-p_i = - \int_0^t p_{u,\rm 21}(t-\tau) \delta q_0 \cdot \delta(\tau) \, d\tau = - p_{u,\rm 01}(t) \cdot \delta q_0\end{array}$

which leads to (1).

Case #2 – Constant BHP: $\begin{array}{l}p_1 = \rm const\end{array}$

Assume that the flowrate in producer W₁ is being automatically adjusted by $\begin{array}{l}\delta q_1(t)\end{array}$ to compensate the bottom-hole pressure variation $\begin{array}{l}\delta p_1(t)\end{array}$ in response to the total sandface flowrate variation $\begin{array}{l}\delta q_2\end{array}$ in injector W₀ so that bottom-hole pressure in producer W₁ stays constant at all times $\begin{array}{l}\delta p_1(t) = \delta p_1 = \rm const\end{array}$ . In petroleum practice this happens when the formation is capable to deliver more fluid than the current lift settings in producer so that the bottom-hole pressure in producer is constantly kept at minimum value defined by the lift design..

In this case, flowrate response $\begin{array}{l}\delta q_1\end{array}$ in producer W₁ to the flowrate variation $\begin{array}{l}\delta q_0\end{array}$ in injector W₀ is going to be:

(7)	$\begin{array}{l}\displaystyle \delta q_1(t) = - \frac{\dot p_{u,\rm 01}(t)}{\dot p_{u,\rm 11}(t)} \cdot \delta q_0\end{array}$

where

$\begin{array}{l}t\end{array}$	time since injector's W₀ rate has changed by $\begin{array}{l}\delta q_0\end{array}$ .
$\begin{array}{l}\dot p_{u,\rm 01}(t)\end{array}$	time derivative of cross-well pressure transient response (CTR) in producer W₁ to the unit-rate production in injector W₀
$\begin{array}{l}\dot p_{u,\rm 11}(t)\end{array}$	time derivative of drawdown pressure transient response (DTR) in producer W₁ to the unit-rate production in the same well

Derivation

Consider a pressure convolution equation for the above 2-wells system with constant BHP:

(8)	$\begin{array}{l}\displaystyle p_1(t) = p_i - \int_0^t p_{u,\rm 11}(t-\tau) dq_1(\tau) - \int_0^t p_{u,\rm 01}(t-\tau) dq_0(\tau) = \rm const\end{array}$

The time derivative is going to be zero as the BHP in producer W₁ stays constant at all times:

(9)	$\begin{array}{l}\displaystyle \dot p_1(t) = - \left( \int_0^t p_{u,\rm 11}(t-\tau) dq_1(\tau) \right)^{\cdot} - \left( \int_0^t p_{u,\rm 01}(t-\tau) dq_0(\tau) \right)^{\cdot} = 0\end{array}$

(10)	$\begin{array}{l}\displaystyle p_{u,\rm 11}(0) \cdot q_1(t) + \int_0^t \dot p_{u,\rm 11}(t-\tau) dq_1(\tau) = - p_{u,\rm 01}(0) \cdot q_0(t) - \int_0^t \dot p_{u,\rm 01}(t-\tau) dq_0(\tau)\end{array}$

The zero-time value of DTR / CTR is zero by definition $\begin{array}{l}p_{u,\rm 11}(0) = 0, \, p_{u,\rm 01}(0) = 0\end{array}$ which leads to:

(11)	$\begin{array}{l}\displaystyle \int_0^t \dot p_{u,\rm 11}(t-\tau) dq_1(\tau) = - \int_0^t \dot p_{u,\rm 21}(t-\tau) dq_2(\tau)\end{array}$

Consider a step-change in producer's W₁ flowrate $\begin{array}{l}\delta q_1\end{array}$ and injector's W₀ flowrate $\begin{array}{l}\delta q_0\end{array}$ at zero time $\begin{array}{l}\tau = 0\end{array}$ , which can be written as $\begin{array}{l}dq_1(\tau) = \delta q_1 \cdot \delta(\tau) \, d\tau\end{array}$ .

Assume that a lift mechanism in producer automatically adjusts the flowrate to maintain the same flowing bottom-hole and $\begin{array}{l}dq_0(\tau) = \delta q_0 \cdot \delta(\tau) \, d\tau\end{array}$ . Substituting this to (11) leads to:

(12)	$\begin{array}{l}\displaystyle \int_0^t \dot p_{u,\rm 11}(t-\tau) \delta q_1 \cdot \delta(\tau) \, d\tau = - \int_0^t \dot p_{u,\rm 01}(t-\tau) \delta q_0 \cdot \delta(\tau) \, d\tau\end{array}$

(13)	$\begin{array}{l}\displaystyle \dot p_{u,\rm 11}(t) \delta q_1 = - \dot p_{u,\rm 01}(t) \delta q_0\end{array}$

which leads to (7).

For the finite-volume drain $\begin{array}{l}V_{\phi,1} \leq V_{\phi,0} < \infty\end{array}$ the flowrate response factor $\begin{array}{l}\delta q_1 / \delta q_0\end{array}$ is getting stabilised over time as:

(14)	$\begin{array}{l}\displaystyle \delta q_1 / \delta q_0 = - f_{01} = - \frac{V_{\phi, 1}}{ V_{\phi, 0}} = \rm const\end{array}$

The response delay in time still exists but in usual time-scales of production analysis it becomes negligible and one can consider (14) as constant in time.

Derivation

For the finite-volume reservoir $\begin{array}{l}V_{\phi,1} \leq V_{\phi,0} < \infty\end{array}$ the DTR and CTR are both going through the PSS flow regime at late transient times:

(15)	$\begin{array}{l}\displaystyle p_{u,\rm 11}(t \rightarrow \infty) \rightarrow \frac{t}{c_t V_{\phi, 1}}\end{array}$

(16)	$\begin{array}{l}\displaystyle p_{u,\rm 01}(t \rightarrow \infty) \rightarrow \frac{t}{c_t V_{\phi,2}}\end{array}$

where

$\begin{array}{l}c_t\end{array}$	average drain-area total compressibility of formation within $\begin{array}{l}V_{\phi,1}\end{array}$ which is jointly drained by producer W₁ and injector W₀

Substituting (15) and (16) in (7) one arrives to (14).

In case injector W₀ supports only one producer W₁, then both wells drain the same reservoir volume $\begin{array}{l}V_{\phi, 0} = V_{\phi, 1}\end{array}$ so that (14) leads to:

(17)	$\begin{array}{l}\displaystyle \delta q_1 = -\delta q_0\end{array}$

which means that producer W₁ with constant BHP and finite-reservoir volume will eventually vary its rate at the same volume as injector W₀.

In case injector W₀ supports many producers {W₁ .. W_N} then all injection shares towards producers are going to sum up to a unit value:

(18)	$\begin{array}{l}\displaystyle \sum_{k=1}^N f_{0k} = 1\end{array}$

with constant coefficients $\begin{array}{l}f_{0k} \geq 0, \ {k=\{i..N \} }\end{array}$ , unless there is a thief injection outside the drainage area of all producers and in this case:

(19)	$\begin{array}{l}\displaystyle \sum_{k=1}^N f_{0k} < 1\end{array}$

If pressure around producer W₁ is supported by several injectors $\begin{array}{l}N_{\rm inj} > 1\end{array}$ then production response in producer W₁ is going to be:

(20)	$\begin{array}{l}\displaystyle \delta q_1 =-\sum_i f_{i1} \delta q_i\end{array}$

with constant coefficients $\begin{array}{l}f_{i1} \geq 0, \ {i=\{0..N_{\rm inj} \} }\end{array}$ .

The equations (18), (19) and (20) make one of the key assumptions in Capacitance Resistance Model (CRM).

It is important to note that CRM assumption that injector W₀ may drain bigger volume than producer W₁ $\begin{array}{l}V_{\phi, 0}> V_{\phi, 1}\end{array}$ is a misnomer in most practical cases.

When wells (producers and injectors) are placed into the same connected reservoir volume they drain the same total volume $\begin{array}{l}V_\phi\end{array}$ all together and all UTRs will have the same LTR asymptotic:

(21)	$\begin{array}{l}\displaystyle p_{u,\rm ik}(t \rightarrow \infty ) \rightarrow \frac{t}{\rm RS}, \quad \forall i \in N_{\rm inj}, k \in N.\end{array}$

where $\begin{array}{l}\rm RS = \int_V c_t \, \phi \, dV\end{array}$ is total reservoir storage connecting all the wells.

Moreover, if each well is placed in different reservoir volumes which are only connected through wellbores then again they will all drain the same volume which is the sum of all connected volumes through the wellbores and all UTRs will again trend to the same LTR asymptotic.

In order to relate true UTRs (from numerical grid simulations or from deconvolution) to the CRM injection share constants $\begin{array}{l}f_{ik}\end{array}$ one needs to implement a certain workflow:

Start with true UTRs $\begin{array}{l}\displaystyle p_{u, ik}(t)\end{array}$ with the same LTR asymptotic $\begin{array}{l}\displaystyle p_{u, ik}(t) \rightarrow \frac{t}{RS}\end{array}$ .
Select injector W₀
1. Select producer W₁
  1. Perform two convolution tests to account for the impact from {W₂ .. W_N} production on to DTR_11 $\begin{array}{l}p_{u, 11}(t)\end{array}$ and CTR_01 $\begin{array}{l}p_{u, 01}(t)\end{array}$ :
    - Test #1 – DTR_11
      - Calculate historically-averaged rate for each producer: $\begin{array}{l}\displaystyle q^*_k = \frac{1}{N_k} \sum_{m=1}^{N_k} q_k(t_m)\end{array}$
      - Calculate interfering DTR_11: $\begin{array}{l}\displaystyle p^*_{u, 11}(t) = p_{u, 11}(t) + \sum_{k \neq 1} p_{u, k1}(t) \cdot q^*_k\end{array}$ , meaning that injector W₀ is shut-down and all producers are working with constant rates $\begin{array}{l}q^*_k\end{array}$ , except producer W₁ which is working with unit-rate
    - Test #2 – CTR_01
      - Calculate historically-averaged rate for each producer: $\begin{array}{l}\displaystyle q^*_k = \frac{1}{N_k} \sum_{m=1}^{N_k} q_k(t_m)\end{array}$
      - Calculate interfering CTR_01: $\begin{array}{l}\displaystyle p^*_{u, 01}(t) = p_{u, 01}(t) + \sum_{k} p_{u, k1}(t) \cdot q^*_k\end{array}$ , meaning that injector W₀ is working with unit-rate and all producers are working with constant rates $\begin{array}{l}q^*_k\end{array}$
  2. Calculate injection share constant: $\begin{array}{l}\displaystyle f_{01} = \frac{\dot p^*_{01}(t)}{\dot p^*_{11}(t)} \Bigg|_{t \rightarrow \infty}\end{array}$ as LLS over equation: $\begin{array}{l}\displaystyle \dot p^*_{01}(t) = f_{01} \cdot \dot p^*_{11}(t)\end{array}$
2. Repeat the same for other producers (starting from point 2a onwards)
Repeat the same for other injectors (starting from point 2 onwards)

Again it is important to note a difference between

CRM assumptions (constant PI, constant drainage volumes with no flow boundaries and constant total compressibility) – which may or may not take place and hence may or may not make CRM applicable in a specific case

and

CRM concept of mismatching drainage volumes between producers and injectors which is just a terminology and does not exert restrictions on well-reservoir system

Page tree

Case #1 – Constant flowrate production: $\begin{array}{l}q_1 = \rm const >0\end{array}$

Case #2 – Constant BHP: $\begin{array}{l}p_1 = \rm const\end{array}$

See also

Page tree

Production – Injection Pairing @ model

Case #1 – Constant flowrate production: q_1 = \rm const >0//<![CDATA[ \begin{array}{l}q_1 = \rm const >0\end{array} //]]>

Case #2 – Constant BHP: p_1 = \rm const//<![CDATA[ \begin{array}{l}p_1 = \rm const\end{array} //]]>

See also

Case #1 – Constant flowrate production: $\begin{array}{l}q_1 = \rm const >0\end{array}$

Case #2 – Constant BHP: $\begin{array}{l}p_1 = \rm const\end{array}$