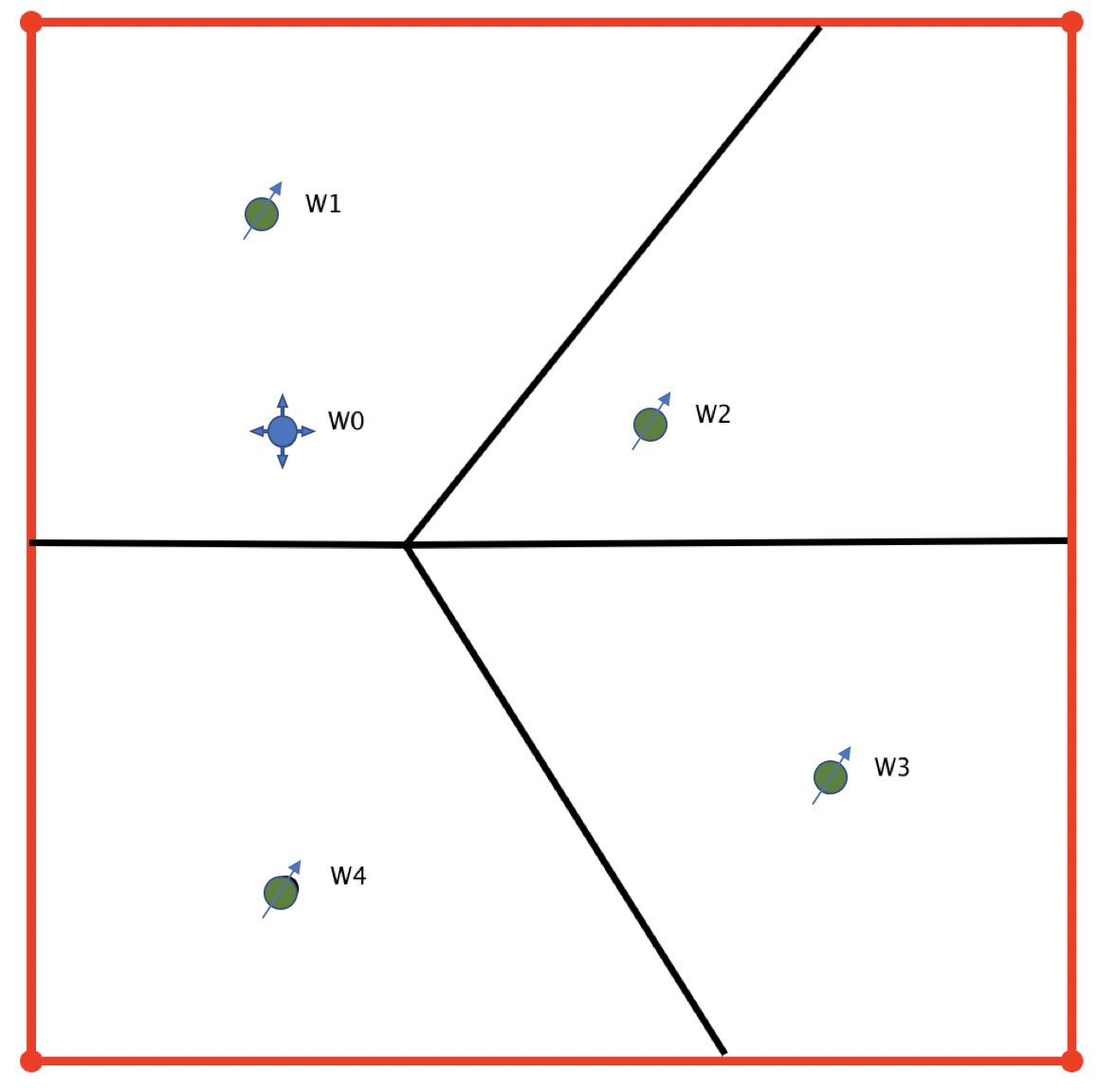
Consider a well-reservoir system (Fig. 1) consisting of:

producing well W₁ with total sandface flowrate $\begin{array}{l}q_1(t)>0\end{array}$ and BHP $\begin{array}{l}p_1(t)>0\end{array}$ , draining the reservoir volume $\begin{array}{l}V_{\phi, 1}\end{array}$
water injecting well W₀ with total sandface flowrate $\begin{array}{l}q_0(t) < 0\end{array}$ , supporting pressure in reservoir volume $\begin{array}{l}V_{\phi, 0}\end{array}$

The injection drainage volume $\begin{array}{l}V_{\phi, 0}\end{array}$ includes the drainage volume $\begin{array}{l}V_{\phi, 1}\end{array}$ of producer W₁ and may be equal to it $\begin{array}{l}V_{\phi, 0} = V_{\phi, 1}\end{array}$ or may be bigger $\begin{array}{l}V_{\phi, 0} > V_{\phi, 1}\end{array}$ in case injector W₀ supports other producers {W₁ .. W_N}: $\begin{array}{l}V_{\phi, 0} = \sum_{k=1}^N V_{\phi, k}\end{array}$ .

Fig. 1. Location map of injector-producer pairing with 4 producers {W₁, W₂, W₃, W₄} and one injector W₀.

Case #1 – Constant flowrate production: $\begin{array}{l}q_1 = \rm const >0\end{array}$

The bottom-hole pressure response $\begin{array}{l}\delta p_1\end{array}$ in producer W₁ to the flowrate variation $\begin{array}{l}\delta q_0\end{array}$ in injector W₀:

(1)	$\begin{array}{l}\displaystyle \delta p_1 = - p_{u,\rm 21}(t) \cdot \delta q_2\end{array}$

where

$\begin{array}{l}t\end{array}$	time since the water injection rate has changed by the $\begin{array}{l}\delta q_2\end{array}$ value.
$\begin{array}{l}p_{u,\rm 01}(t)\end{array}$	cross-well pressure transient response in producer W₁ to the unit-rate production in injector W₀

Derivation

Consider a pressure convolution equation for the BHP in producer W₁with constant flowrate production at producer W₁ $\begin{array}{l}q_1 = \rm const\end{array}$ and varying injection rate at injector W₂ $\begin{array}{l}q_2(t)\end{array}$ :

(2)	$\begin{array}{l}\displaystyle p_1(t) = p_i - \int_0^t p_{u,\rm 11}(t-\tau) dq_1(\tau) - \int_0^t p_{u,\rm 01}(t-\tau) dq_0(\tau) = p_i - \int_0^t p_{u,\rm 01}(t-\tau) dq_0(\tau)\end{array}$

Consider a step-change in injector's W₀ flowrate $\begin{array}{l}\delta q_0\end{array}$ at zero time $\begin{array}{l}\tau = 0\end{array}$ , which can be written as: $\begin{array}{l}dq_0 (\tau) = \delta q_0 \cdot \delta(\tau) \, d\tau\end{array}$ .

The responding pressure variation $\begin{array}{l}\delta p_1\end{array}$ in producer W₁will be:

(3)	$\begin{array}{l}\displaystyle \delta p_1(t) = p_1(t)-p_i = - \int_0^t p_{u,\rm 21}(t-\tau) \delta q_0 \cdot \delta(\tau) \, d\tau = - p_{u,\rm 01}(t) \cdot \delta q_0\end{array}$

which leads to (1).

Case #2 – Constant BHP: $\begin{array}{l}p_1 = \rm const\end{array}$

Assume that the flowrate in producer W₁ is being automatically adjusted by $\begin{array}{l}\delta q_1(t)\end{array}$ to compensate the bottom-hole pressure variation $\begin{array}{l}\delta p_1(t)\end{array}$ in response to the total sandface flowrate variation $\begin{array}{l}\delta q_2\end{array}$ in injector W₀ so that bottom-hole pressure in producer W₁ stays constant at all times $\begin{array}{l}\delta p_1(t) = \delta p_1 = \rm const\end{array}$ . In petroleum practice this happens when the formation is capable to deliver more fluid than the current lift settings in producer so that the bottom-hole pressure in producer is constantly kept at minimum value defined by the lift design..

In this case, flowrate response $\begin{array}{l}\delta q_1\end{array}$ in producer W₁ to the flowrate variation $\begin{array}{l}\delta q_0\end{array}$ in injector W₀ is going to be:

(4)	$\begin{array}{l}\displaystyle \delta q_1(t) = - \frac{\dot p_{u,\rm 01}(t)}{\dot p_{u,\rm 11}(t)} \cdot \delta q_0\end{array}$

where

$\begin{array}{l}t\end{array}$	time since injector's W₀ rate has changed by $\begin{array}{l}\delta q_0\end{array}$ .
$\begin{array}{l}\dot p_{u,\rm 01}(t)\end{array}$	time derivative of cross-well pressure transient response (CTR) in producer W₁ to the unit-rate production in injector W₀
$\begin{array}{l}\dot p_{u,\rm 11}(t)\end{array}$	time derivative of drawdown pressure transient response (DTR) in producer W₁ to the unit-rate production in the same well

Derivation

Consider a pressure convolution equation for the above 2-wells system with constant BHP:

(5)	$\begin{array}{l}\displaystyle p_1(t) = p_i - \int_0^t p_{u,\rm 11}(t-\tau) dq_1(\tau) - \int_0^t p_{u,\rm 01}(t-\tau) dq_0(\tau) = \rm const\end{array}$

The time derivative is going to be zero as the BHP in producer W₁ stays constant at all times:

(6)	$\begin{array}{l}\displaystyle \dot p_1(t) = - \left( \int_0^t p_{u,\rm 11}(t-\tau) dq_1(\tau) \right)^{\cdot} - \left( \int_0^t p_{u,\rm 01}(t-\tau) dq_0(\tau) \right)^{\cdot} = 0\end{array}$

(7)	$\begin{array}{l}\displaystyle p_{u,\rm 11}(0) \cdot q_1(t) + \int_0^t \dot p_{u,\rm 11}(t-\tau) dq_1(\tau) = - p_{u,\rm 01}(0) \cdot q_0(t) - \int_0^t \dot p_{u,\rm 01}(t-\tau) dq_0(\tau)\end{array}$

The zero-time value of DTR / CTR is zero by definition $\begin{array}{l}p_{u,\rm 11}(0) = 0, \, p_{u,\rm 01}(0) = 0\end{array}$ which leads to:

(8)	$\begin{array}{l}\displaystyle \int_0^t \dot p_{u,\rm 11}(t-\tau) dq_1(\tau) = - \int_0^t \dot p_{u,\rm 21}(t-\tau) dq_2(\tau)\end{array}$

Consider a step-change in producer's W₁ flowrate $\begin{array}{l}\delta q_1\end{array}$ and injector's W₀ flowrate $\begin{array}{l}\delta q_0\end{array}$ at zero time $\begin{array}{l}\tau = 0\end{array}$ , which can be written as $\begin{array}{l}dq_1(\tau) = \delta q_1 \cdot \delta(\tau) \, d\tau\end{array}$ .

Assume that a lift mechanism in producer automatically adjusts the flowrate to maintain the same flowing bottom-hole and $\begin{array}{l}dq_0(\tau) = \delta q_0 \cdot \delta(\tau) \, d\tau\end{array}$ . Substituting this to (8) leads to:

(9)	$\begin{array}{l}\displaystyle \int_0^t \dot p_{u,\rm 11}(t-\tau) \delta q_1 \cdot \delta(\tau) \, d\tau = - \int_0^t \dot p_{u,\rm 01}(t-\tau) \delta q_0 \cdot \delta(\tau) \, d\tau\end{array}$

(10)	$\begin{array}{l}\displaystyle \dot p_{u,\rm 11}(t) \delta q_1 = - \dot p_{u,\rm 01}(t) \delta q_0\end{array}$

which leads to (4).

For the finite-volume drain $\begin{array}{l}V_{\phi,1} \leq V_{\phi,0} < \infty\end{array}$ the flowrate response factor $\begin{array}{l}\delta q_1 / \delta q_0\end{array}$ is getting stabilised over time as:

(11)	$\begin{array}{l}\displaystyle \delta q_1 / \delta q_0 = - f_{01} = - \frac{V_{\phi, 1}}{ V_{\phi, 0}} = \rm const\end{array}$

The response delay in time still exists but in usual time-scales of production analysis it becomes negligible and one can consider (11) as constant in time.

Derivation

For the finite-volume reservoir $\begin{array}{l}V_{\phi,1} \leq V_{\phi,0} < \infty\end{array}$ the DTR and CTR are both going through the PSS flow regime at late transient times:

(12)	$\begin{array}{l}\displaystyle p_{u,\rm 11}(t \rightarrow \infty) \rightarrow \frac{t}{c_t V_{\phi, 1}}\end{array}$

(13)	$\begin{array}{l}\displaystyle p_{u,\rm 01}(t \rightarrow \infty) \rightarrow \frac{t}{c_t V_{\phi,2}}\end{array}$

where

$\begin{array}{l}c_t\end{array}$	average drain-area total compressibility of formation within $\begin{array}{l}V_{\phi,1}\end{array}$ which is jointly drained by producer W₁ and injector W₀

Substituting (12) and (13) in (4) one arrives to (11).

In case injector W₀ supports only one producer W₁ , then both wells drain the same volume and $\begin{array}{l}V_{\phi, 0} = V_{\phi, 1}\end{array}$ so that (11) leads to:

(14)	$\begin{array}{l}\displaystyle \delta q_1 = -\delta q_0\end{array}$

which means that producer W₁ with constant BHP and finite-reservoir volume will eventually vary its rate at the same volume as injector W₀.

In case injector W₀ supports many producers {W₁ .. W_N} then all injection shares towards producers are going to sum up to a unit value:

(15)	$\begin{array}{l}\displaystyle \sum_{k=1}^N f_{0k} = 1\end{array}$

unless there is thief injection outside the drain area of all producers and in this case:

(16)	$\begin{array}{l}\displaystyle \sum_{k=1}^N f_{0k} < 1\end{array}$

If pressure in producer W₁ is supported by several injectors $\begin{array}{l}N_{\rm inj} > 1\end{array}$ then over a long period of time one can assume:

(17)	$\begin{array}{l}\displaystyle \delta q_1 =\sum_k f_{k1} \delta q_k\end{array}$

with constant coefficients $\begin{array}{l}f_{1k}, \ {k=\{1..N_{\rm inj} \} }\end{array}$ , which makes one of the key assumptions in Capacitance Resistance Model (CRM).

Page tree

Case #1 – Constant flowrate production: $\begin{array}{l}q_1 = \rm const >0\end{array}$

Case #2 – Constant BHP: $\begin{array}{l}p_1 = \rm const\end{array}$

See also

Page tree

Production – Injection Pairing

Case #1 – Constant flowrate production: q_1 = \rm const >0//<![CDATA[ \begin{array}{l}q_1 = \rm const >0\end{array} //]]>

Case #2 – Constant BHP: p_1 = \rm const//<![CDATA[ \begin{array}{l}p_1 = \rm const\end{array} //]]>

See also

Case #1 – Constant flowrate production: $\begin{array}{l}q_1 = \rm const >0\end{array}$

Case #2 – Constant BHP: $\begin{array}{l}p_1 = \rm const\end{array}$