Content

Definition

Mathematical model of multiphase wellbore flow predicts the temperature, pressure and flow speed distribution along the wellbore trajectory with account for:

tubing head pressure which is set by gathering system or injection pump
wellbore design
pump characterisits
fluid friction with tubing /casing walls
interfacial phase slippage
heat exchange between wellbore fluid and surrounding rocks

Mathematical Model

The multiphase wellbore flow is defined by the following set of 1D equations:

(1)	$\begin{array}{l}\displaystyle \frac{\partial (\rho_m A)}{\partial t} + \frac{\partial}{\partial l} \bigg( A \, \sum_\alpha \rho_\alpha \, u_\alpha \bigg) = 0\end{array}$

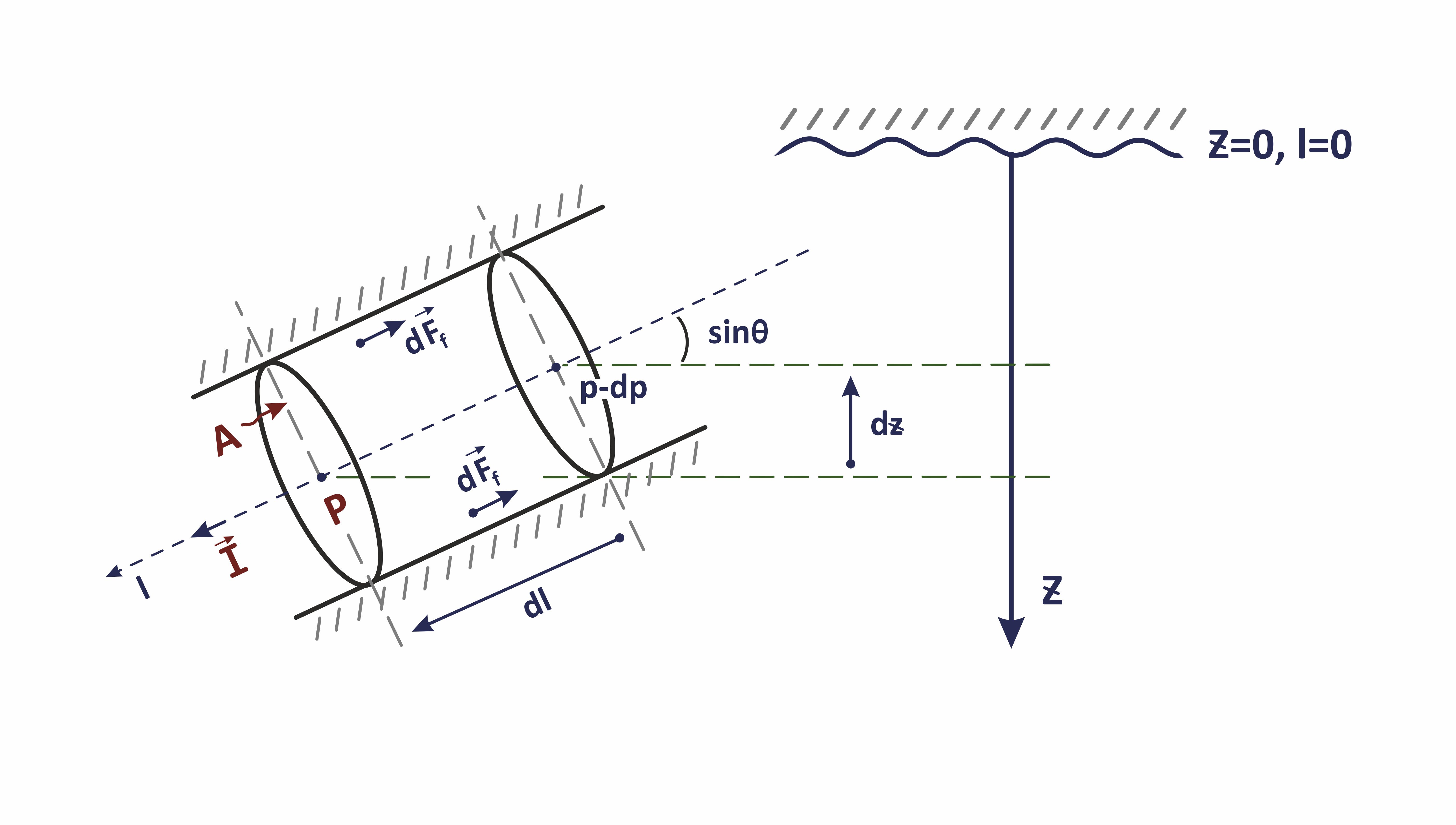
(2)	$\begin{array}{l}\displaystyle \sum_\alpha \rho_\alpha \bigg[ \frac{\partial u_\alpha}{\partial t} + u_\alpha \frac{\partial u_\alpha}{\partial l} - \nu_\alpha \Delta u_\alpha\bigg] = - \frac{dp}{dl} + \rho_m \, g \, \sin \theta - \frac{ f_m \, \rho_m \, u_m^2 \, }{2 d}\end{array}$

(3)

$\begin{array}{l}\displaystyle (\rho \,c_p)_m \frac{\partial T}{\partial t} - \sum_\alpha \rho_\alpha \ c_{p \alpha} \ \eta_{s \alpha} \ \frac{\partial P_\alpha}{\partial t} + \sum_\alpha \rho_\alpha \ c_{p \alpha} \ u_\alpha \frac{\partial T}{\partial l} \ = \ \frac{1}{A} \ \sum_\alpha \rho_\alpha \ c_{p \alpha} T_\alpha \frac{\partial q_\alpha}{\partial l}\end{array}$

where

$\begin{array}{l}m\end{array}$	indicates a mixture of fluid phases
$\begin{array}{l}\alpha = \{w,o,g \}\end{array}$	water, oil, gas phase indicator
$\begin{array}{l}l\end{array}$	measure length along wellbore trajectory
$\begin{array}{l}\rho_m(l)\end{array}$	cross-sectional average fluid density
$\begin{array}{l}\theta(l)\end{array}$	wellbore trajectory inclination to horizon
$\begin{array}{l}d(l)\end{array}$	cross-sectional average pipe flow diameter
$\begin{array}{l}A(l)\end{array}$	in-situ cross-sectional area $\begin{array}{l}A(l) = 0.25 \, \pi \, d^2(l)\end{array}$
$\begin{array}{l}f(l)\end{array}$	Darci flow friction coefficient
$\begin{array}{l}\nu_\alpha\end{array}$	kinematic viscosity of $\begin{array}{l}\alpha\end{array}$ -phase

Equations (1) – (3) define a closed set of 3 scalar equations on 3 unknowns: pressure $\begin{array}{l}p(l)\end{array}$ , temperature $\begin{array}{l}T(l)\end{array}$ and fluid velocity $\begin{array}{l}u(l)\end{array}$ .

The model is set in 1D-model with $\begin{array}{l}l-\end{array}$ axis aligned with well trajectory $\begin{array}{l}l(x,y,z)\end{array}$ :

The disambiguation of the properties in the above equation is brought in The list of dynamic flow properties and model parameters.

Equation (1) defines the continuity of the fluid components flow or equivalently represent the mass conservation of each mass component $\begin{array}{l}\{ m_W, \ m_O, \ m_G \}\end{array}$ during its transportation along wellbore.

Equation (2) defines the motion dynamics of each phase (called Navier–Stokes equation), represented as linear correlation between phase flow speed $\begin{array}{l}u_\alpha\end{array}$ and pressure profile of mutliphase fluid $\begin{array}{l}p\end{array}$ .

The term $\begin{array}{l}\sum_\alpha \rho_\alpha \ c_{p \alpha} \ u_\alpha \frac{\partial T}{\partial l}\end{array}$ represents heat convection defined by the wellbore mass flow.

The term $\begin{array}{l}\sum_\alpha \rho_\alpha \ c_{p \alpha} \ \eta_{s \alpha} \ \frac{\partial P_\alpha}{\partial t}\end{array}$ represents the heating/cooling effect of the fast adiabatic pressure change.

This usually takes effect in the wellbore during the first minutes or hours after changing the well flow regime (as a consequence of choke/pump operation).

Derivation

(4)

$\begin{array}{l}\displaystyle (\rho \,c_{pt})_p \frac{\partial T}{\partial t} - \sum_{a = \{w,o,g \}} \rho_\alpha \ c_{p \alpha} \ \eta_{s \alpha} \ \frac{\partial P_\alpha}{\partial t} + \sum_{a = \{w,o,g \}} \rho_\alpha \ c_{p \alpha} \ u_\alpha \frac{\partial T}{\partial l} \ = \ \frac{\delta E_H}{ \delta V \delta t}\end{array}$

Equation (3) defines the heat flow continuity or equivalently represents heat conservation due to heat conduction and convection with account for adiabatic and Joule–Thomson throttling effect.

The term $\begin{array}{l}\frac{\delta E_H}{ \delta V \delta t}\end{array}$ defines the speed of change of heat energy $\begin{array}{l}E_H\end{array}$ volumetric density due to the inflow from formation into the wellbore.

Stationary Flow Model

Stationary wellbore flow is defined as the flow with constant pressure and temperature: $\begin{array}{l}\frac{\partial T}{\partial t} = 0\end{array}$ and $\begin{array}{l}\frac{\partial P_\alpha}{\partial t} = 0\end{array}$ .

This happens during the long-term (usually hours & days & weeks) production/injection or long-term (usually hours & days & weeks) shut-in.

The temperature dynamic equation (3) is going to be:

(5)	$\begin{array}{l}\displaystyle \sum_\alpha \rho_\alpha \ c_{p \alpha} \ u_\alpha \frac{\partial T}{\partial l} \ = \ \frac{1}{A} \ \sum_\alpha \rho_\alpha \ c_{p \alpha} T_\alpha \frac{\partial q_\alpha}{\partial l}\end{array}$

The phase temperature $\begin{array}{l}T_\alpha\end{array}$ is the temperature of the $\begin{array}{l}\alpha\end{array}$ -phase flowing from reservoir into wellbore.

It carries the original reservoir temperature with heating/cooling effect from reservoir-flow throttling and well-reservoir contact throttling:

(6)	$\begin{array}{l}\displaystyle T_\alpha = T_r + \epsilon_\alpha \, \delta P = T_r + \epsilon_\alpha \, (P_e - P_{wf})\end{array}$

The discrete computational scheme for (5) will be:

(7)

$\begin{array}{l}\displaystyle \bigg( \sum_\alpha \rho_\alpha^{k-1} \ c_{p \alpha}^{k-1} \ q_\alpha^{k-1} \bigg) T^{k-1} - \bigg( \sum_\alpha \rho_\alpha^k \ c_{p \alpha}^k \ q_\alpha^k \bigg) T^k = \sum_\alpha \rho_\alpha^k \ c_{p \alpha}^k \ (q_\alpha^{k-1} - q_\alpha^k) \, (T_r^k + \epsilon_\alpha^k \delta p^k )\end{array}$

where $\begin{array}{l}\delta p^k = p_e^k - p_{wf}^k\end{array}$ is drawdown, $\begin{array}{l}p_e^k\end{array}$ – formation pressure in $\begin{array}{l}k\end{array}$ -th grid layer, $\begin{array}{l}p_{wf}^k\end{array}$ – bottom-hole pressure across $\begin{array}{l}k\end{array}$ -th grid layer, $\begin{array}{l}T_r^k\end{array}$ – remote reservoir temperature of $\begin{array}{l}k\end{array}$ -th grid layer.

The $\begin{array}{l}l\end{array}$ -axis is pointing downward along hole with $\begin{array}{l}(k-1)\end{array}$ -th grid layer sitting above the $\begin{array}{l}k\end{array}$ -th grid layer.

If the flowrate is not vanishing during the stationary lift ( $\begin{array}{l}\sum_{a = \{w,o,g \}} |q_\alpha^{k-1}| > 0\end{array}$ ) then $\begin{array}{l}T^{k-1}\end{array}$ can be calculated iteratively from previous values of the wellbore temperature $\begin{array}{l}T^k\end{array}$ as:

(8)

$\begin{array}{l}\displaystyle T^{k-1} = \frac{\bigg( \sum_\alpha \rho_\alpha^k \ c_{p \alpha}^k \ q_\alpha^k \bigg) T^k + \sum_\alpha \rho_\alpha^k \ c_{p \alpha}^k \ (q_\alpha^{k-1} - q_\alpha^k) \, (T_r^k + \epsilon_\alpha^k \delta p^k )}{\bigg( \sum_\alpha \rho_\alpha^{k-1} \ c_{p \alpha}^{k-1} \ q_\alpha^{k-1} \bigg) }\end{array}$

Deduction

(9)

$\begin{array}{l}\displaystyle (\rho \,c_{pt})_p \frac{\partial T}{\partial t} - \ \phi \sum_{a = \{w,o,g \}} \rho_\alpha \ c_{p \alpha} \ \eta_{s \alpha} \ \frac{\partial P_\alpha}{\partial t} + \bigg( \sum_{a = \{w,o,g \}} \rho_\alpha \ c_{p \alpha} \ \epsilon_\alpha \ \mathbf{u}_\alpha \bigg) \nabla P + \bigg( \sum_{a = \{w,o,g \}} \rho_\alpha \ c_{p \alpha} \ \mathbf{u}_\alpha \bigg) \ \nabla T - \nabla (\lambda_t \nabla T) = \frac{\delta E_H}{ \delta V \delta t}\end{array}$

The wellbore fluid velocity $\begin{array}{l}u_\alpha\end{array}$ can be expressed thorugh the volumetric flow profile $\begin{array}{l}q_\alpha\end{array}$ and tubing/casing cross-section area $\begin{array}{l}\pi r_f^2\end{array}$ as:

(10)	$\begin{array}{l}\displaystyle u_\alpha = \frac{q_\alpha}{\pi r_f^2}\end{array}$

so that

(11)	$\begin{array}{l}\displaystyle \bigg( \sum_{a = \{w,o,g \}} \rho_\alpha \ c_{p \alpha} \ \mathbf{u}_\alpha \bigg) \ \nabla T = \frac{\delta E_H}{ \delta V \delta t}\end{array}$

References

Beggs, H. D. and Brill, J. P.: "A Study of Two-Phase Flow in Inclined Pipes," J. Pet. Tech., May (1973), 607-617

The list of dynamic flow properties and model parameters

$\begin{array}{l}(t,x,y,z)\end{array}$	time and space corrdinates , $\begin{array}{l}z\end{array}$ -axis is orientated towards the Earth centre, $\begin{array}{l}(x,y)\end{array}$ define transversal plane to the $\begin{array}{l}z\end{array}$ -axis
$\begin{array}{l}\mathbf{r} = (x, \ y, \ z)\end{array}$	position vector at which the flow equations are set
$\begin{array}{l}l (x, \ y, \ z)\end{array}$	measured depth along borehole trajectory $\begin{array}{l}dl^2 = dx^2 + dy^2 + dz^2\end{array}$ starting from tubing head $\begin{array}{l}l (x = x_0, \ y=y_0, \ z = z_{THP}) = 0\end{array}$
$\begin{array}{l}q_{mW} = \frac{d m_W}{dt}\end{array}$	speed of water-component mass change in wellbore draining points
$\begin{array}{l}q_{mO} = \frac{d m_O}{dt}\end{array}$	speed of oil-component mass change in wellbore draining points
$\begin{array}{l}q_{mG} = \frac{d m_G}{dt}\end{array}$	speed of gas-component mass change in wellbore draining points
$\begin{array}{l}q_W = \frac{1}{\rho_W^{\LARGE \circ}} \frac{d m_W}{dt} = \frac{d V_{Ww}^{\LARGE \circ}}{dt} = \frac{1}{B_w} q_w\end{array}$	volumetric water-component flow rate in wellbore draining points recalculated to standard surface conditions
$\begin{array}{l}q_O = \frac{1}{\rho_O^{\LARGE \circ}} \frac{d m_O}{dt} = \frac{d V_{Oo}^{\LARGE \circ}}{dt} + \frac{d V_{Og}^{\LARGE \circ}}{dt} = \frac{1}{B_o} q_o + \frac{R_v}{B_g} q_g\end{array}$	volumetric oil-component flow rate in wellbore draining points recalculated to standard surface conditions
$\begin{array}{l}q_G = \frac{1}{\rho_G^{\LARGE \circ}} \frac{d m_G}{dt} = \frac{d V_{Gg}^{\LARGE \circ}}{dt} + \frac{d V_{Go}^{\LARGE \circ}}{dt} = \frac{1}{B_g} q_g + \frac{R_s}{B_o} q_o\end{array}$	volumetric gas-component flow rate in wellbore draining points recalculated to standard surface conditions
$\begin{array}{l}q_w = \frac{d V_w}{dt}\end{array}$	volumetric water-phase flow rate in wellbore draining points
$\begin{array}{l}q_o = \frac{d V_o}{dt}\end{array}$	volumetric oil-phase flow rate in wellbore draining points
$\begin{array}{l}q_g = \frac{d V_g}{dt}\end{array}$	volumetric gas-phase flow rate in wellbore draining points
$\begin{array}{l}q^S_W =\frac{dV_{Ww}^S}{dt}\end{array}$	total well volumetric water-component flow rate
$\begin{array}{l}q^S_O = \frac{d (V_{Oo}^S + V_{Og}^S )}{dt}\end{array}$	total well volumetric oil-component flow rate
$\begin{array}{l}q^S_G = \frac{d (V_{Gg}^S + V_{Go}^S )}{dt}\end{array}$	total well volumetric gas-component flow rate
$\begin{array}{l}q^S_L = q^S_W + q^S_O\end{array}$	total well volumetric liquid-component flow rate
$\begin{array}{l}\vec u_w = \vec u_w (t, \vec r)\end{array}$	water-phase flow speed distribution and dynamics
$\begin{array}{l}\vec u_o = \vec u_o (t, \vec r)\end{array}$	oil-phase flow speed distribution and dynamics
$\begin{array}{l}\vec u_g = \vec u_g (t, \vec r)\end{array}$	gas-phase flow speed distribution and dynamics
$\begin{array}{l}\vec g = (0, \ 0, \ g)\end{array}$	gravitational acceleration vector
$\begin{array}{l}g = 9.81 \ \rm m/s^2\end{array}$	gravitational acceleration constant
$\begin{array}{l}\rho_\alpha(P,T)\end{array}$	mass density of $\begin{array}{l}\alpha\end{array}$ -phase fluid
$\begin{array}{l}\mu_\alpha(P,T)\end{array}$	viscosity of $\begin{array}{l}\alpha\end{array}$ -phase fluid
$\begin{array}{l}\lambda_t(P,T,s_w, s_o, s_g)\end{array}$	effective thermal conductivity of the rocks with account for multiphase fluid saturation
$\begin{array}{l}\lambda_r(P,T)\end{array}$	rock matrix thermal conductivity
$\begin{array}{l}\lambda_\alpha(P,T)\end{array}$	thermal conductivity of $\begin{array}{l}\alpha\end{array}$ -phase fluid
$\begin{array}{l}\rho_r(P,T)\end{array}$	rock matrix mass density
$\begin{array}{l}\eta_{s \alpha}(P,T)\end{array}$	differential adiabatic coefficient of $\begin{array}{l}\alpha\end{array}$ -phase fluid
$\begin{array}{l}c_{pr}(P,T)\end{array}$	specific isobaric heat capacity of the rock matrix
$\begin{array}{l}c_{p\alpha}(P,T)\end{array}$	specific isobaric heat capacity of $\begin{array}{l}\alpha\end{array}$ -phase fluid
$\begin{array}{l}\epsilon_\alpha (P, T)\end{array}$	differential Joule–Thomson coefficient of $\begin{array}{l}\alpha\end{array}$ -phase fluid дифференциальный коэффициент Джоуля-Томсона фазы $\begin{array}{l}\alpha\end{array}$

Page tree

Wellbore Multiphase Flow

Definition

Mathematical Model

Stationary Flow Model

References

The list of dynamic flow properties and model parameters