...
The Inflow Performance Relation (IPR) analysis is closely related to well Productivity Index (PI)
which is defined as below:
| LaTeX Math Block |
|---|
| J_s(q_O) = \frac{q_O}{p_r-p_{wf}} |
|
for oil producer with oil flowrate at surface conditions |
| LaTeX Math Block |
|---|
| J_s(q_G) = \frac{q_G}{p_r-p_{wf}} |
|
for gas producer with gas flowrate at surface conditions |
| LaTeX Math Block |
|---|
| J_s(q_{GI}) = \frac{q_{GI}}{p_{wf}-p_r} |
|
for gas injector with injection rate at surface conditions |
| LaTeX Math Block |
|---|
| J_s(q_{WI}) = \frac{q_{WI}}{p_r-p_{wf}} |
|
for water injector with injection rate at surface conditions |
where
Based on above defintions the aribitrary IPR can be wirtten in a general form:
...
providing that
has a specific meaning and sign as per the table below:
| for producer |
| for injector |
| for oil producer |
| for gas producer or injector |
| for water injector or water producer or water production from oil producer |
See more on the variations of PI definition between Dynamic Modelling, Well Flow Performance and Well Testing.
...
For a single layer formation with low-compressibility fluid (water or dead oil) the PI does not depend on drawdown (or flowrate)
and
IPR plot is reperented by a straight line (Fig. 1)
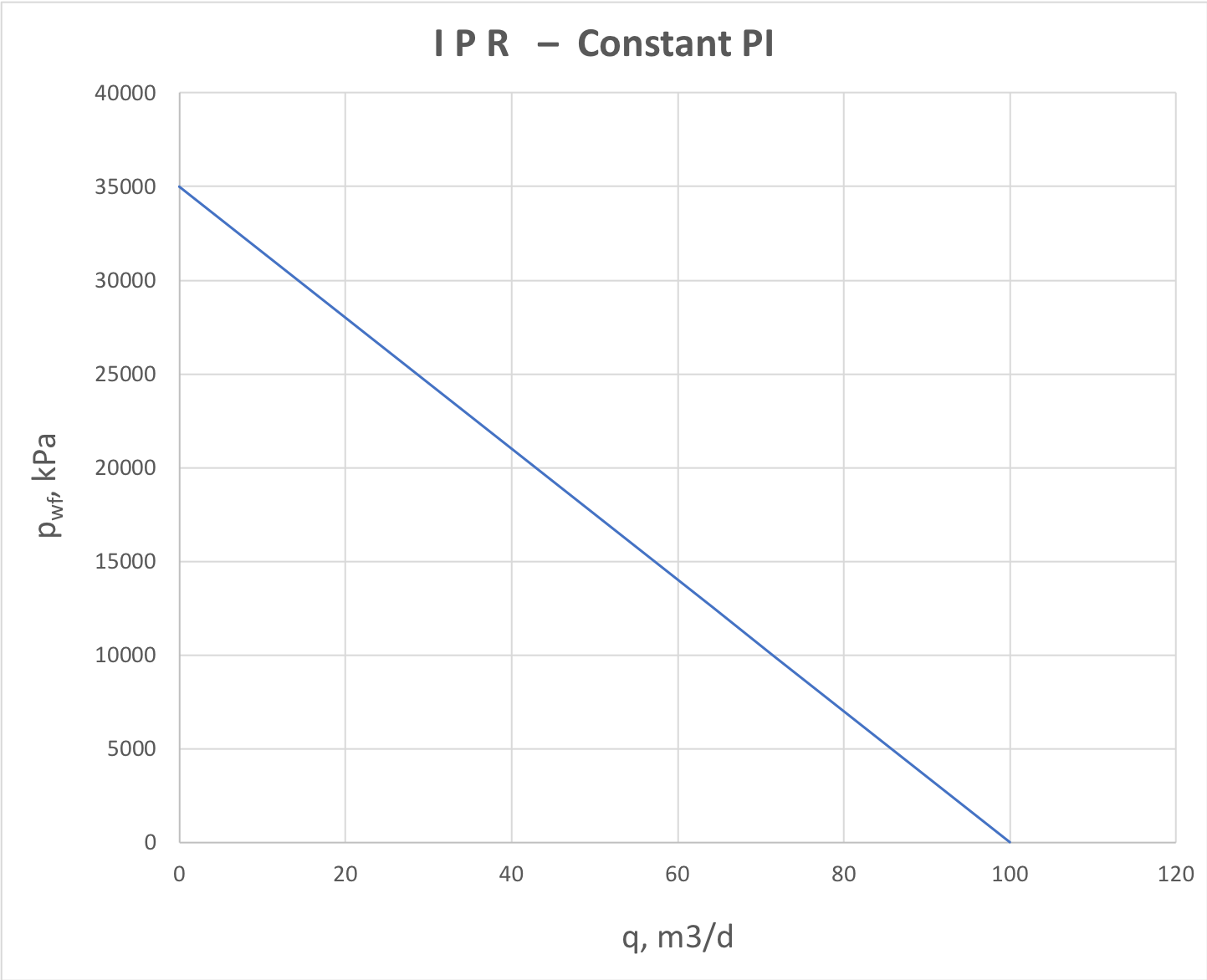 Image Modified Image Modified
|
| Fig.1. IPR plot for constant productivity (water and dead oil) |
This is a typical IPR plot for water supply wells, water injectors and dead oil producers.
...
For gas producers, the fluid compressibility is high and formation flow is essentially non-linear, inflicting the downward trend on the whole IPR plot (Fig. 2).
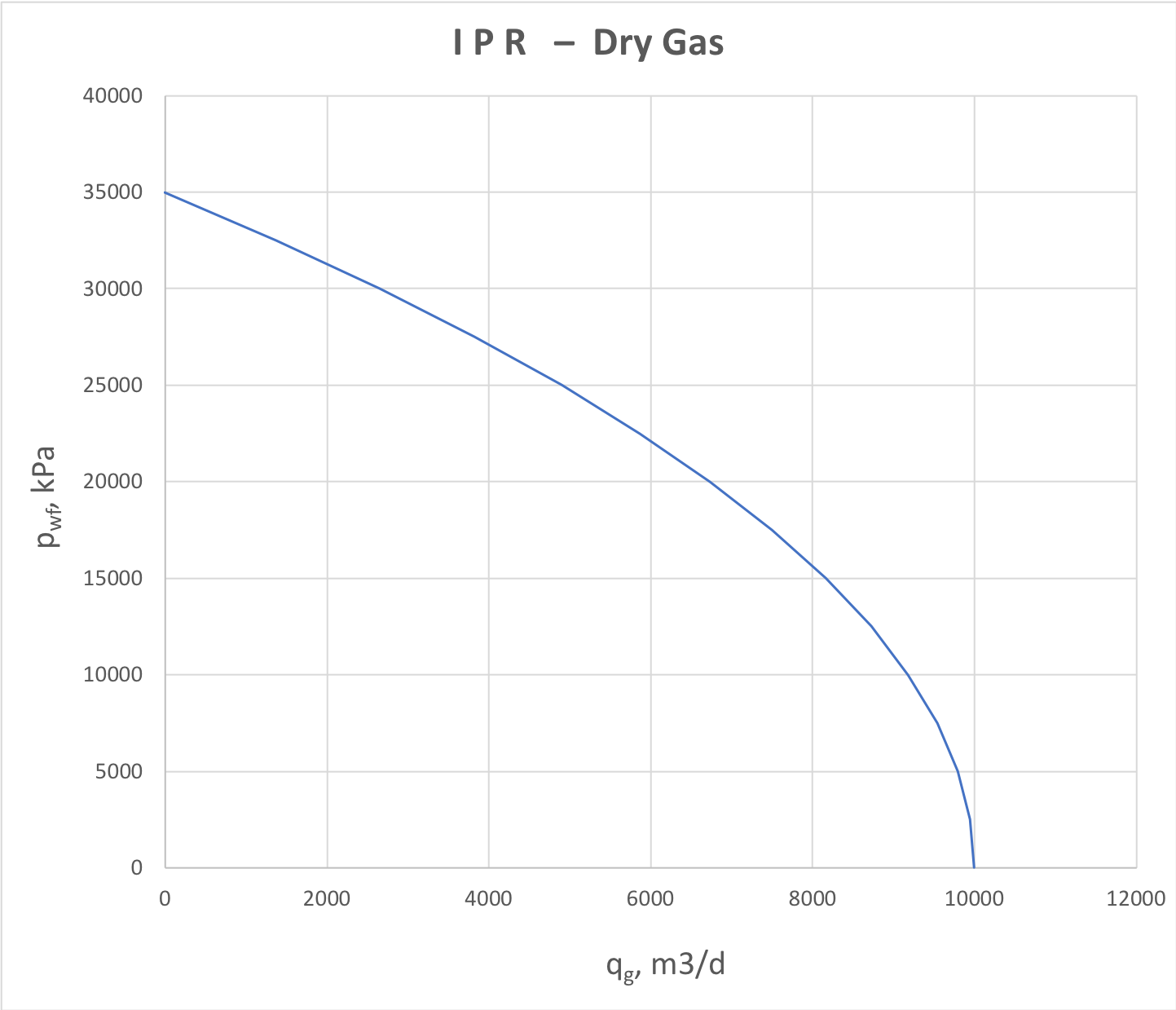 Image Modified Image Modified
|
Fig. 2. IPR for dry gas producer or gas injector into a gas formation |
The popular dry gas IPR correlation is Rawlins and Shellhardt:
...
For saturated oil reservoir the free gas flow inflict the downward trend of IPR plot similar to dry gas (Fig. 3).
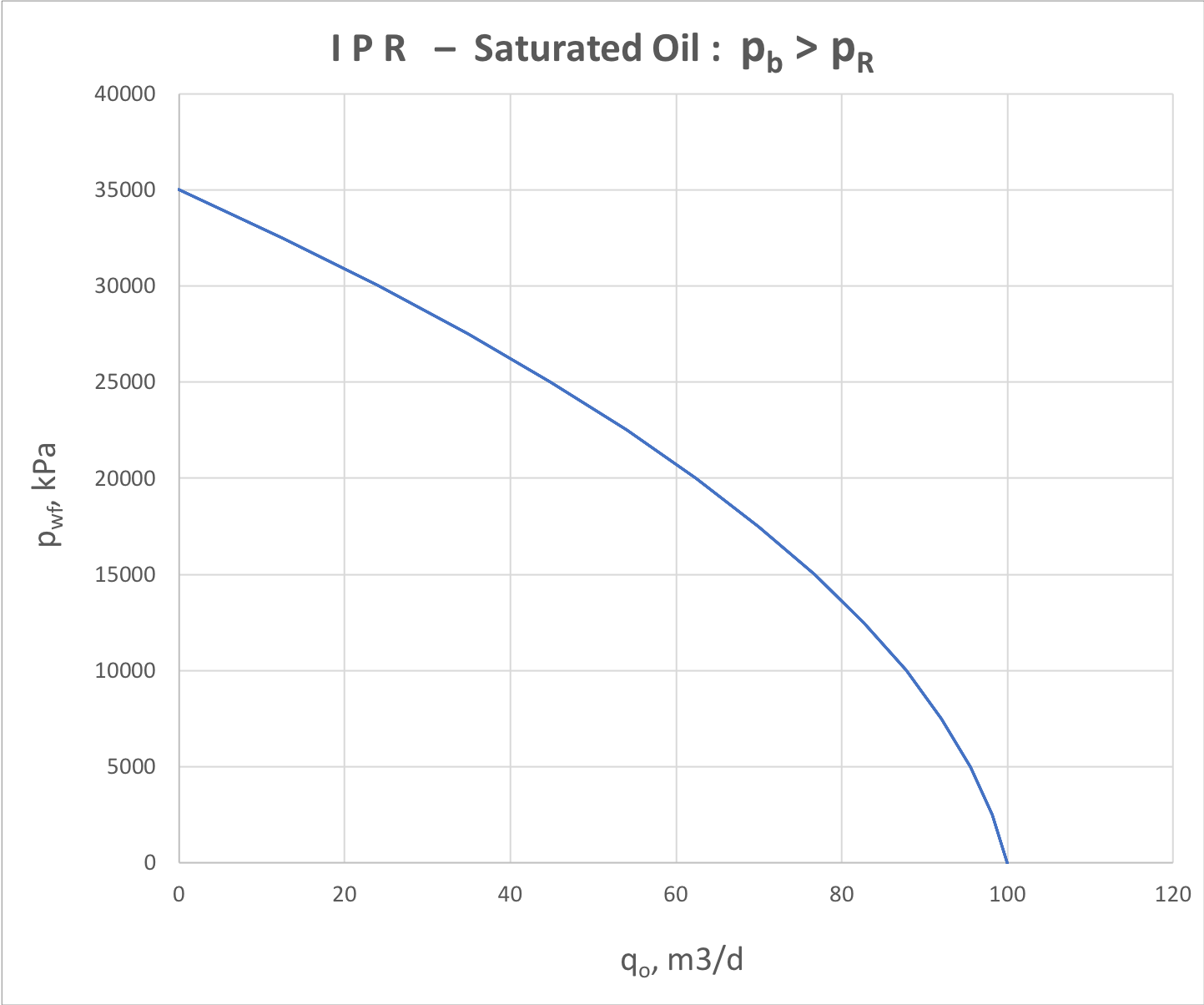 Image Modified Image Modified
|
Fig. 3. IPR for 2-phase oil+gas production below and above bubble point |
The analytical correlation for saturted oil flow is given by Vogel model:
| Excerpt Include |
|---|
| Vogel IPR model |
|---|
| Vogel IPR model |
|---|
| nopanel | true |
|---|
|
| LaTeX Math Block |
|---|
|
\frac{q}{q_{max}} = 1 - 0.2 \, \frac{p_{wf}}{p_r} - 0.8 \Bigg(\frac{p_{wf}}{p_r} \Bigg)^2 \quad , \quad p_b > p_r > p_{wf} |
...
It can be interpreted as deterioration of near-reservoir zone permeability when the fluid velocity is high and approximated by rate-dependant skin-factor.
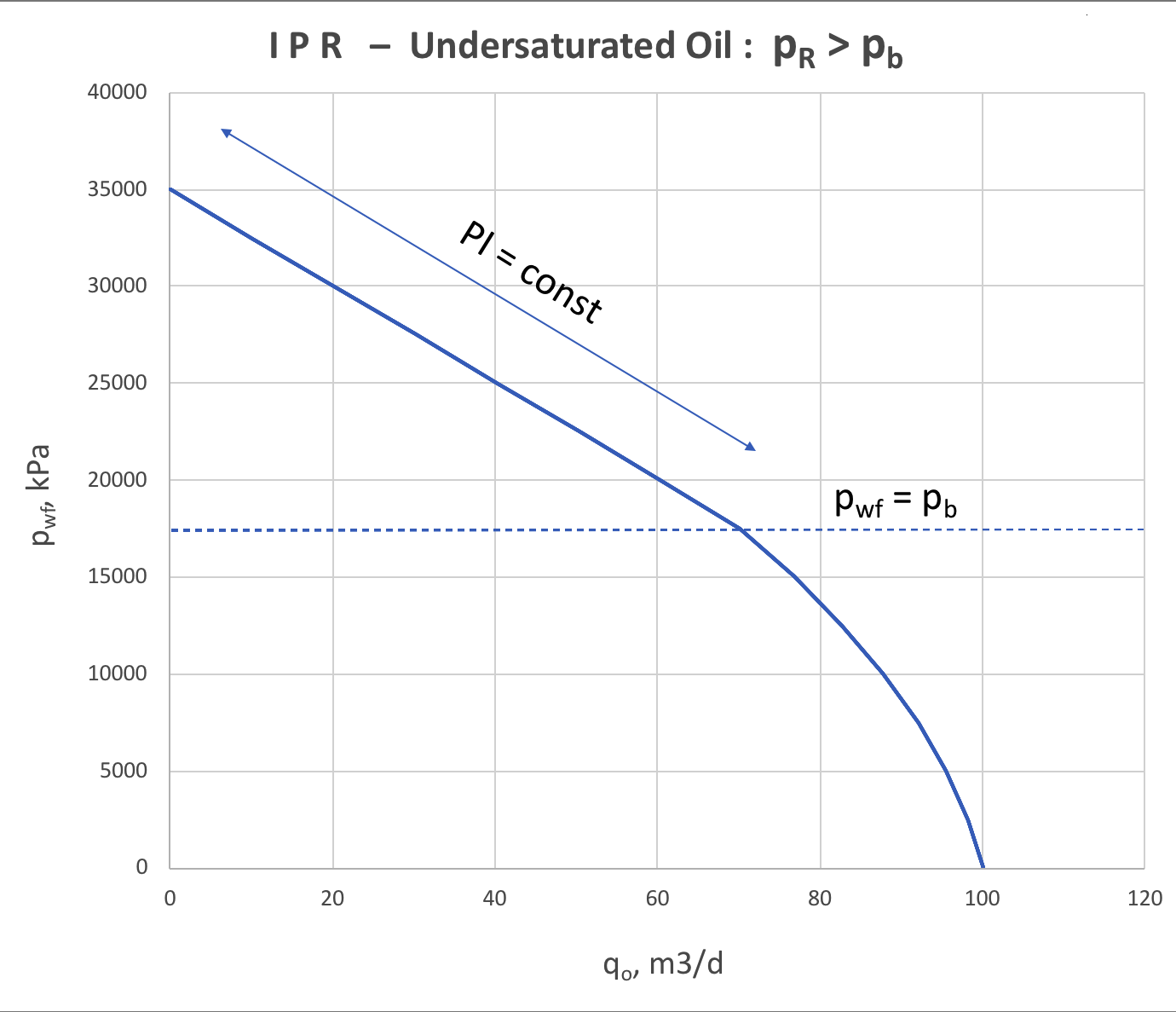 Image Modified Image Modified
|
Fig. 3. IPR for 2-phase oil+gas production below and above bubble point |
The analytical correlation for undersaturated oil flow is given by modified Vogel model:
...
For saturated 3-phase water-oil-gas reservoir the IPR analysis is represented by oil and water components separately (see Fig. 4.1 and Fig. 4.2).
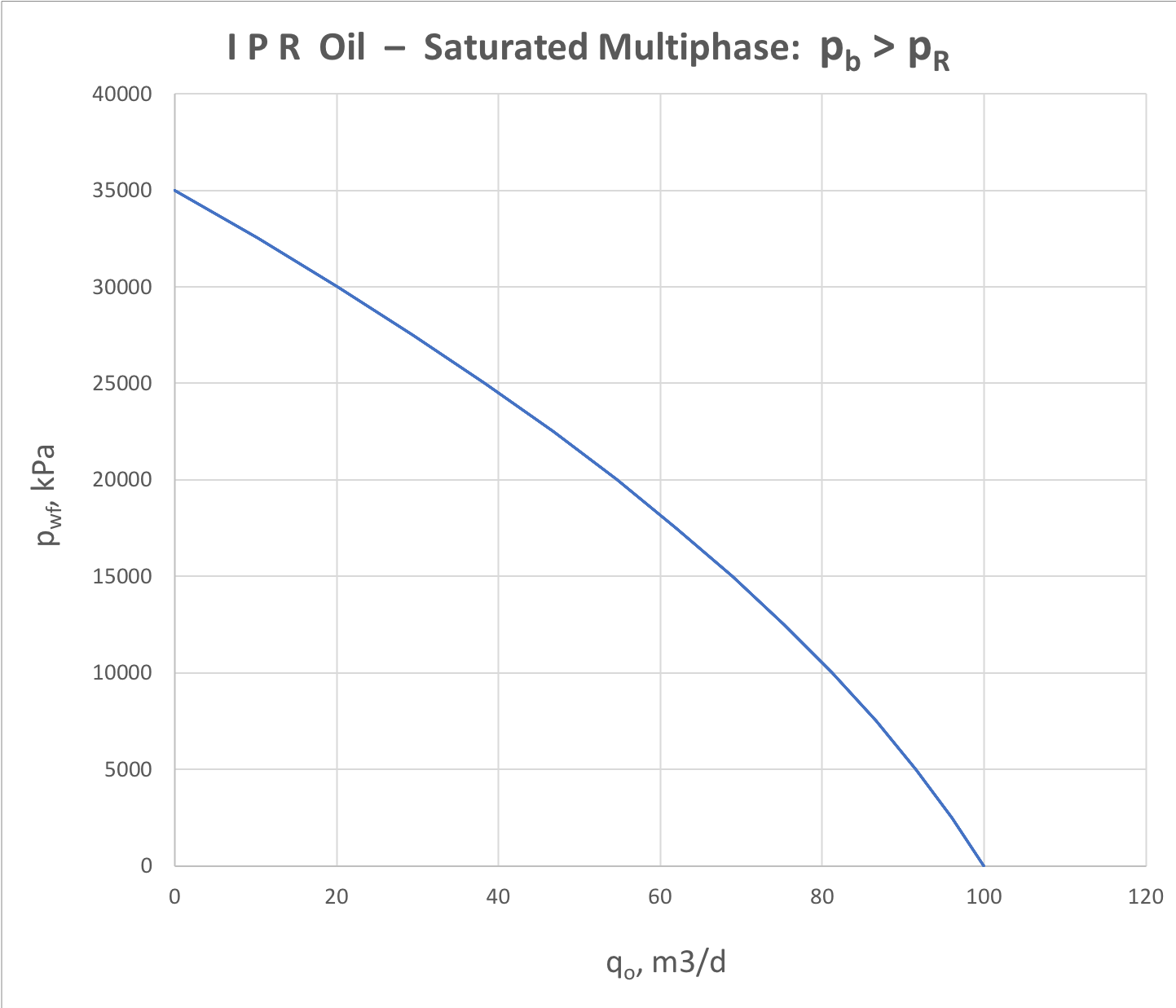 Image Modified Image Modified
| 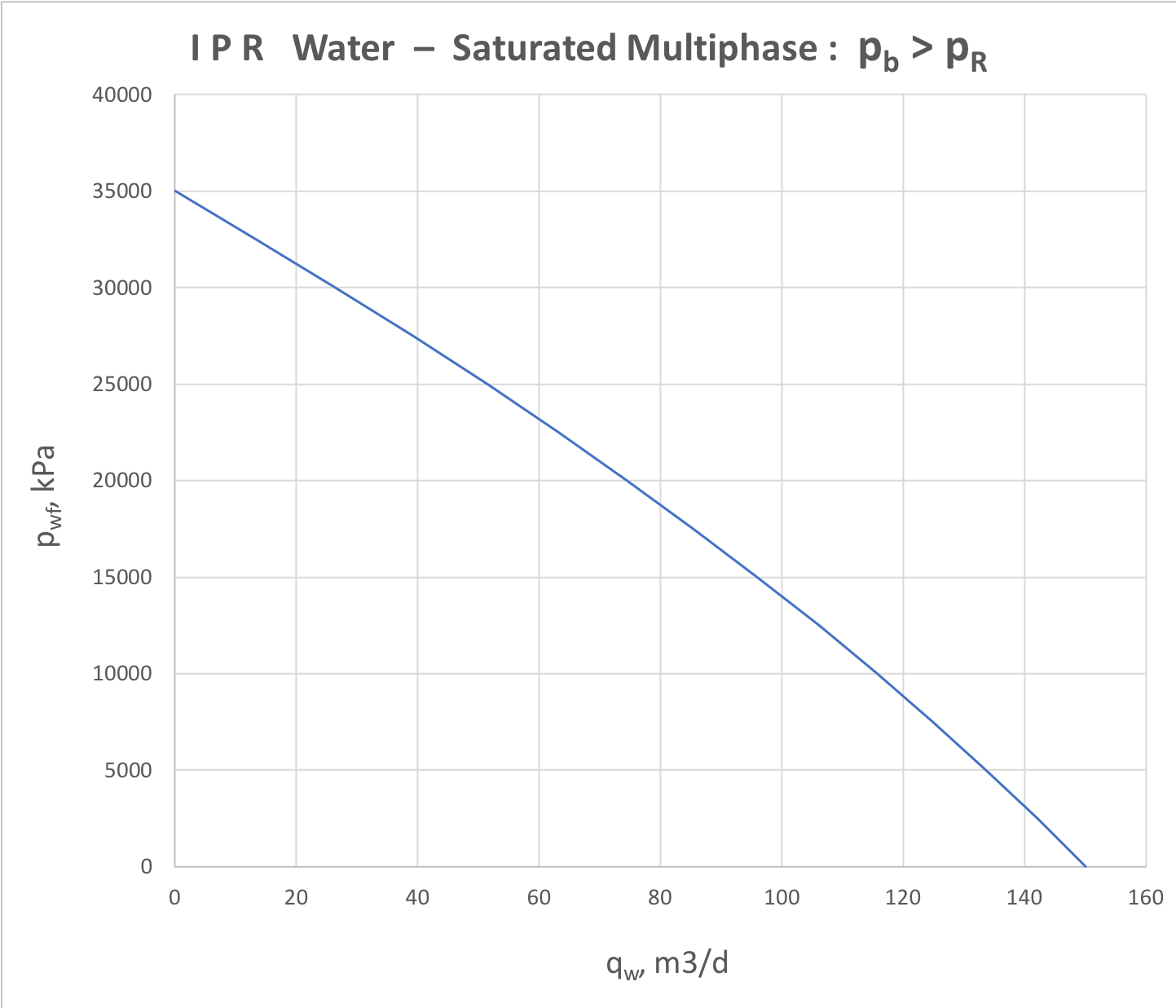 Image Modified Image Modified
|
Fig. 4.1. Oil IPR for saturated 3-phase (water + oil + gas) formation flow | Fig. 4.2. Water IPR for saturated 3-phase (water + oil + gas) formation flow |
The analytical correlation for saturated 3-phase oil flow is given by Wiggins model:
...
For undersaturated 3-phase water-oil-gas reservoir the IPR analysis is represented by oil and water components separately (see Fig. 4.1 and Fig. 4.2).
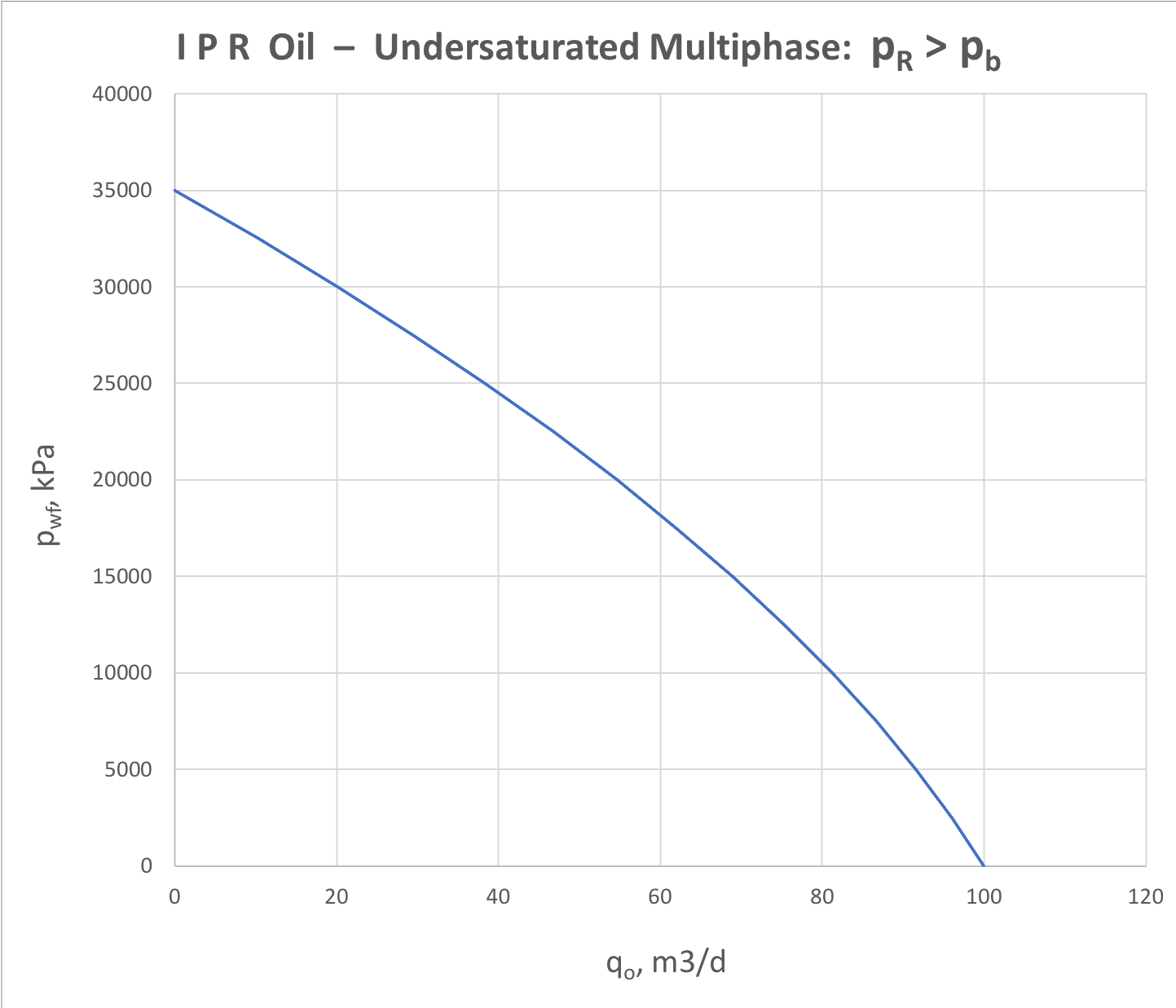 Image Modified Image Modified
| 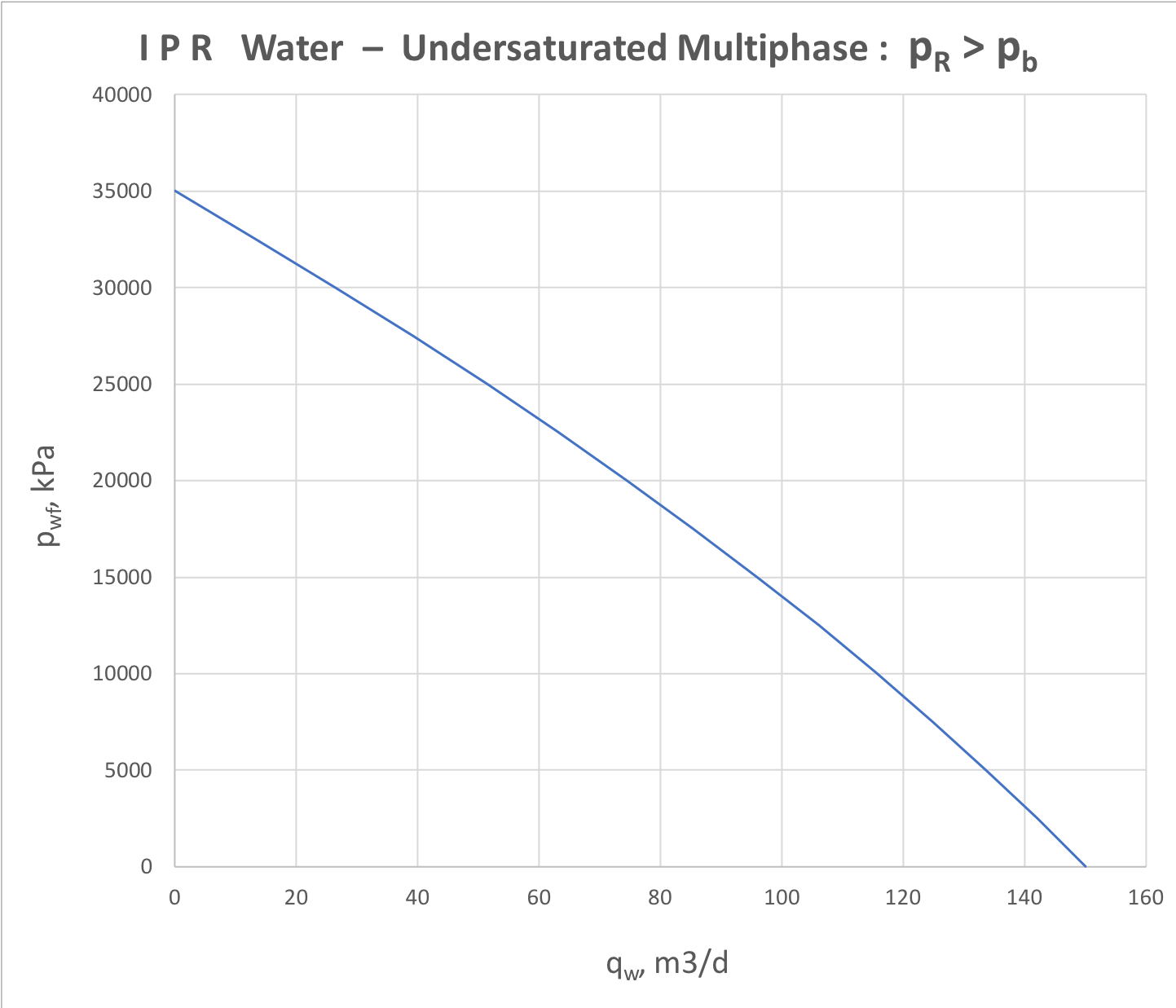 Image Modified Image Modified
|
Fig. 4.1. Oil IPR for udersaturated 3-phase (water + oil + gas) formation flow | Fig. 4.2. Water IPR for undersaturated 3-phase (water + oil + gas) formation flow |
| Show If |
|---|
|
The analytical correlation for saturated 3-phase oil flow is given by Wiggins model: | LaTeX Math Block |
|---|
| \frac{q_o}{q_{o, \, max}} = 1 - 0.52 \, \frac{p_{wf}}{p_r} - 0.48 \Bigg(\frac{p_{wf}}{p_r} \Bigg)^2 |
| LaTeX Math Block |
|---|
| \frac{q_w}{q_{w, \, max}} = 1 - 0.72 \, \frac{p_{wf}}{p_r} - 0.28 \Bigg(\frac{p_{wf}}{p_r} \Bigg)^2 |
|
...







