Consider a system of net hydrocarbon pay and aquifer as a radial composite reservoir with inner composite area being a Net Pay Area and outer composite area an Aquifer.
The transient pressure diffusion flow in this system is going to honour the following equationTransient flow in Radial Composite Reservoir:
| LaTeX Math Block |
|---|
| \frac{\partial p_a}{\partial t} = \chi \cdot \left[ \frac{\partial^2 p_a}{\partial r^2} + \frac{1}{r}\cdot \frac{\partial p_a}{\partial r} \right] |
| | LaTeX Math Block |
|---|
| p_a(t = 0, r)= p(0) |
| | LaTeX Math Block |
|---|
| p_a(t, r=r_e) = p(t) |
| | LaTeX Math Block |
|---|
| anchor | p1_PSS |
|---|
| alignment | left |
|---|
| \frac{\partial p_a}{\partial r}
\bigg|_{(t, r=r_a)} = 0 |
|
Consider a pressure convolution:
| LaTeX Math Block |
|---|
| p_a(t, r) = p(0) + \int_0^t p_1 \left(\frac{(t-\tau) \cdot \chi}{r_e^2}, \frac{r}{r_e} \right) \dot p(\tau) d\tau |
| | LaTeX Math Block |
|---|
| \dot p(\tau) = \frac{d p}{d \tau} |
|
One can easily check that
| LaTeX Math Block Reference |
|---|
|
honors the whole set of equations
| LaTeX Math Block Reference |
|---|
|
–
| LaTeX Math Block Reference |
|---|
|
and as such defines a unique solution of the above problem.
...
| LaTeX Math Block |
|---|
|
Q^{\downarrow}_{AQ}(t) = \theta \cdot h \cdot M \cdot \iint_D d\xi \ d\tau \, \dot p(\tau)
\frac{\partial p_1}{\partial r_D} \left( \frac{(\xi-\tau)\chi}{r_e^2}, r_D \right) \Bigg|_{r_D=1}
|
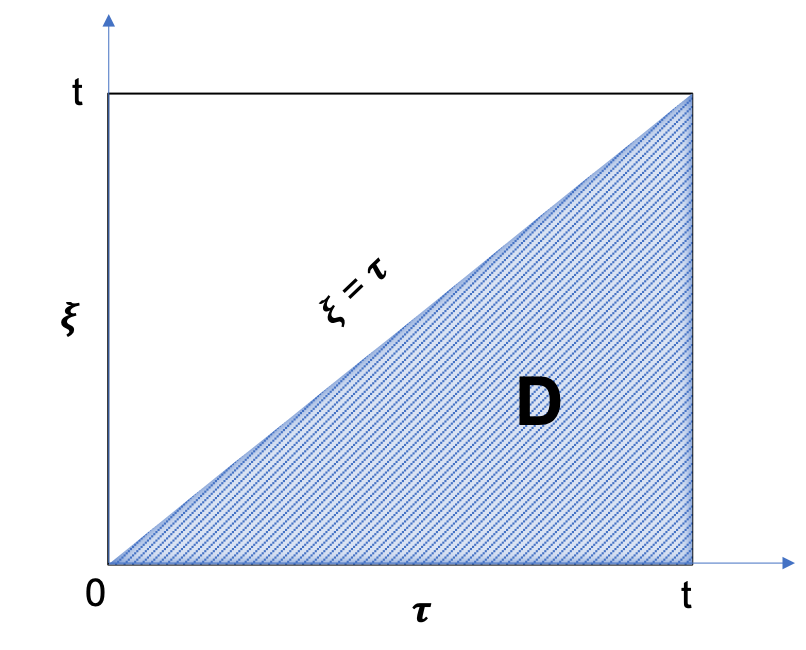 Image Modified Image Modified
|
Fig. 1. Illustration of the integration area in plane |
Changing the integration order from
to
leads to:
...
