@wikipedia
Two different functions of real argument
are called this way:
| LaTeX Math Block |
|---|
| {\rm Ei}(x) = - \int_{-x}^{\infty} \frac{e^{-\xi}}{\xi} \, d\xi |
|
| LaTeX Math Block |
|---|
| {\rm E_1}(x) = \int_{x}^{\infty} \frac{e^{-\xi}}{\xi} \, d\xi |
|
which are related to each other as:
| LaTeX Math Block |
|---|
|
{\rm Ei}(x) = - E_1(-x) |
There is a trend to moving from
definition which was dominating in the past towards
.
|
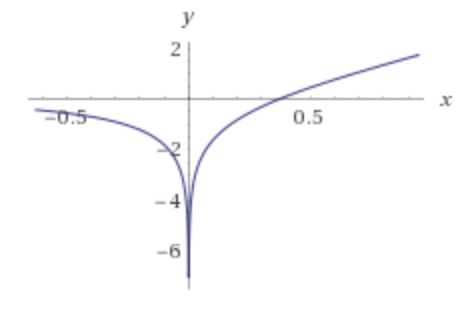
Fig. 1. A sample graph of |
Approximations
| |
|---|
| LaTeX Math Block |
|---|
| {\rm Ei}(x) = \gamma + \ln |x| + \sum_{k=1}^\infty \frac{x^k}{k\cdot k!} |
|
| LaTeX Math Block |
|---|
| {\rm Ei}(x) = e^x \, \left[ \frac{1}{x} + \sum_{k=2}^\infty \frac{(k-1)!}{x^k} \right] |
|
|
|
| |
| LaTeX Math Block |
|---|
| {\rm Ei}(-x) \sim \gamma + \ln x |
|
| LaTeX Math Block |
|---|
| {\rm Ei}(x) \sim \gamma + \ln x |
|
Application
The
-based function:
| LaTeX Math Block |
|---|
|
{\rm w}(t, r) = E_1 \left( \frac{r^2}{4 \, t} \right) = -{\rm Ei} \left( - \frac{r^2}{4 \, t} \right) |
defines a solution planar axial-symmetric diffusion equation:
| LaTeX Math Block |
|---|
| \frac{\partial {\rm w}}{\partial t} = \frac{\partial {\rm w}^2}{\partial^2 r} + \frac{1}{r} \frac{\partial {\rm w}}{\partial r} |
|
| LaTeX Math Block |
|---|
| {\rm w}(t=0, r) = 0 |
|
| LaTeX Math Block |
|---|
| {\rm w}(t, r=\infty) = 0 |
|
| LaTeX Math Block |
|---|
| 0 <= {\rm w}(t, r) < \infty \, , \ \forall (t,r) \in D = \{ t \geq 0, r>0 \}
\subset \mathbb{R} |
|
and is widely used in radial mass-heat transfer simulations.
References
https://www.wolframalpha.com/input/?i=Ei(x)