Consider a system of net hydrocarbon pay and finite or infinite volume Aquifer as a radial composite reservoir with inner composite area being a Net Pay Area and outer composite area an Aquifer

(see schematic and notations on Fig. 1 at Radial VEH Aquifer Drive @model).

The Aquifer's outer boundary may be "no-flow" for finite-volume Aquifer or constant pressure for infinite-volume Aquifer.

The transient pressure diffusion in the outer (Aquifer) composite area is going to honour the following equation:

Driving equationInitial condition

Homogeneous Aquifer reservoir with

Initial Aquifer pressure is considered to be the same as Net Pay Area
\frac{\partial p_a}{\partial t} = \chi \cdot \left[ \frac{\partial^2 p_a}{\partial r^2} + \frac{1}{r}\cdot \frac{\partial p_a}{\partial r} \right]
p_a(t = 0, r)= p(0)



Inner Aquifer boundaryOuter Aquifer boundary is one of the two below:
Pressure variation at the contact with Net Pay Are"No-flow" "Constant pressure" 
p_a(t, r=r_e) = p(t)
\frac{\partial p_a}{\partial r} 
\bigg|_{(t, r=r_a)} = 0
 p_a(t, r = \infty) = 0


Consider dimensionless solution  of the following equation:

\frac{\partial p_1}{\partial t_D} =  \frac{\partial^2 p_1}{\partial r_D^2} + \frac{1}{r_D}\cdot \frac{\partial p_1}{\partial r_D}
p_1(t_D = 0, r_D)= 0



p_1(t_D, r_D=1) = 1
\frac{\partial p_1(t_D, r_D)}{\partial r_D} 
\Bigg|_{r_D=r_{aD}} = 0 \quad {\rm or} \quad  p_1(t_D, r_D = \infty) = 0

which represents a unique function of dimensionless time and distance .


Now consider a convolution integral:

p_a(t, r) = p(0) + \int_0^t p_1 \left(\frac{(t-\tau) \cdot \chi}{r_e^2}, \frac{r}{r_e} \right) \dot p(\tau) d\tau
\dot p(\tau) = \frac{d p}{d \tau}


One can easily check that honours the whole set of equations –/ and as such defines a unique solution of the above problem.

Now having the pressure dynamics in hand one can calculate the water influx.

The water flowrate within sector angle at the interface with net pay is:

q^{\downarrow}_{AQ}(t)= \theta \cdot r_e \cdot h \cdot u(t,r_e)

where is flow velocity at Net Pay ↔ Aquifer contact boundary, which is:

u(t,r_e) = M \cdot \frac{\partial p_a(t,r)}{\partial r} \bigg|_{r=r_e}


where is Aquifer mobility.


The water flowrate is going to be:

q^{\downarrow}_{AQ}(t)= \theta \cdot r_e \cdot h \cdot M \cdot  \frac{\partial p_a(t,r)}{\partial r} \bigg|_{r=r_e}

and cumulative water flux is going to be:

Q^{\downarrow}_{AQ}(t) = \int_0^t q^{\downarrow}_{AQ}(t) dt = \theta \cdot r_e \cdot h \cdot M  \cdot \int_0^t \frac{\partial p_a(t,r)}{\partial r} \bigg|_{r=r_e} dt


Substituting into leads to:

Q^{\downarrow}_{AQ}(t) = \theta  \cdot r_e \cdot h \cdot M  \cdot \int_0^t d\xi \  \frac{\partial }{\partial r} \left[  

\int_0^\xi p_1 \left( \frac{(\xi-\tau)\chi}{r_e^2}, \frac{r}{r_e} \right) \, \dot p(\tau) d\tau

\right]_{r=r_e}  
Q^{\downarrow}_{AQ}(t) = \theta  \cdot h \cdot M  \cdot \int_0^t d\xi \  \frac{\partial }{\partial r_D} \left[  

\int_0^\xi p_1 \left( \frac{(\xi-\tau)\chi}{r_e^2}, r_D \right) \, \dot p(\tau) d\tau

\right]_{r_D=1}   
Q^{\downarrow}_{AQ}(t) = \theta  \cdot h \cdot M  \cdot \int_0^t d\xi \   

\int_0^\xi \frac{\partial p_1}{\partial r_D} \left( \frac{(\xi-\tau)\chi}{r_e^2}, r_D \right) \Bigg|_{r_D=1} \, \dot p(\tau) d\tau

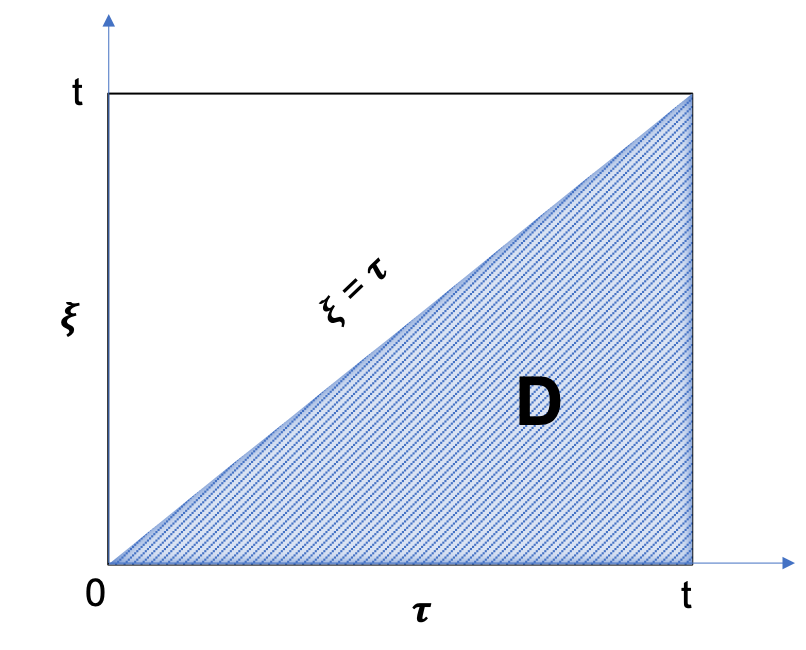
The above integral represents the integration over the area in plane (see Fig. 1):

Q^{\downarrow}_{AQ}(t) = \theta  \cdot h \cdot M  \cdot \iint_D d\xi \ d\tau  \, \dot p(\tau) 

\frac{\partial p_1}{\partial r_D} \left( \frac{(\xi-\tau)\chi}{r_e^2}, r_D \right) \Bigg|_{r_D=1}

Fig. 1. Illustration of the integration area in plane



Changing the integration order from to leads to:

Q^{\downarrow}_{AQ}(t) = \theta  \cdot h \cdot M  \cdot \int_0^t d\tau \int_\tau^t d\xi  \ \dot p(\tau) 

\frac{\partial p_1}{\partial r_D} \left( \frac{(\xi-\tau)\chi}{r_e^2}, r_D \right) \Bigg|_{r_D=1} 
= 
 \theta  \cdot h \cdot M  \cdot \int_0^t \dot p(\tau) d\tau \int_\tau^t d\xi  \ 

\frac{\partial p_1}{\partial r_D} \left( \frac{(\xi-\tau)\chi}{r_e^2}, r_D \right) \Bigg|_{r_D=1}

Replacing the variable:

\xi = \tau + \frac{r_e^2}{\chi} \cdot t_D \rightarrow t_D = \frac{(\xi-\tau)\chi}{r_e^2} \rightarrow d\xi = \frac{r_e^2}{\chi} \cdot dt_D

and cumulative influx becomes:

Q^{\downarrow}_{AQ}(t) = \theta  \cdot h \cdot M \cdot \frac{r_e^2}{\chi} \cdot \int_0^t \dot p(\tau) d\tau \int_0^{(t-\tau)\chi/r_e^2}  

\frac{\partial p_1( t_D, r_D)}{\partial r_D}  \Bigg|_{r_D=1} dt_D = B \cdot \int_0^t \dot p(\tau) d\tau \int_0^{(t-\tau)\chi/r_e^2}  

\frac{\partial p_1( t_D, r_D)}{\partial r_D}  \Bigg|_{r_D=1} dt_D

where 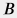is water influx constant and which leads to:

Q^{\downarrow}_{AQ}= B \cdot \int_0^t W_{eD} \left( \frac{(t-\tau)\chi}{r_e^2}\right) \dot p(\tau) d\tau

where

W_{eD}(t) = \int_0^{t} \frac{\partial p_1}{\partial r_D} \bigg|_{r_D = 1} dt_D

is a unique dimensionless function of dimensionless time which can be tabulated via numerical solution or approximated by closed-form expression.


See Also

Petroleum Industry / Upstream / Subsurface E&P Disciplines / Field Study & Modelling / Aquifer Drive / Aquifer Drive Models / Radial VEH Aquifer Drive @model