@wikipedia

Ideally balanced water + dead oil 1D waterflood model without gravity and capillary effects.

\frac{\partial s}{\partial t} + q \cdot \frac{\partial }{\partial x} \left( \frac{f}{\phi \, \Sigma} \right) = 0

s(t=0,x) = 0

s(t,0) = 1

where

	water → oil displacement efficiency
	sandface injection rate, assumed equal to sandface liquid production rate
	reservoir porosity
	cross-section area available for flow
	reservoir thickness
	reservoir width = reservoir length transversal to flow
	in-situ fractional flow function
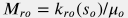	relative oil mobility
	relative water mobility

Approximations

In many practical applications (for example, laboratory SCAL tests and reservoir proxy-modeling) one can assume constant porosity and reservoir width:

\frac{\partial s}{\partial t_D} +\frac{\partial f}{\partial x_D} = 0

s(t=0,x) = 0

s(t,0) = 1

where

	dimensionless time
	dimensionless distance
	reservoir length along -axis
	reservoir pore volume

The equation can be explicitly integrated:

x_D(s) = \begin{cases}\dot f(s) \cdot t, & \mbox{if } s < s^*\\1- \dot f(s) \cdot t, & \mbox{if } s \geq s^*\end{cases}

and used as algebraic equation to find a solution of in terms of saturation over time and distance: .

Reference

Buckley-Leverett.xlsx

Approximations

See Also

Reference