outer radius of tubing (with outer radius )
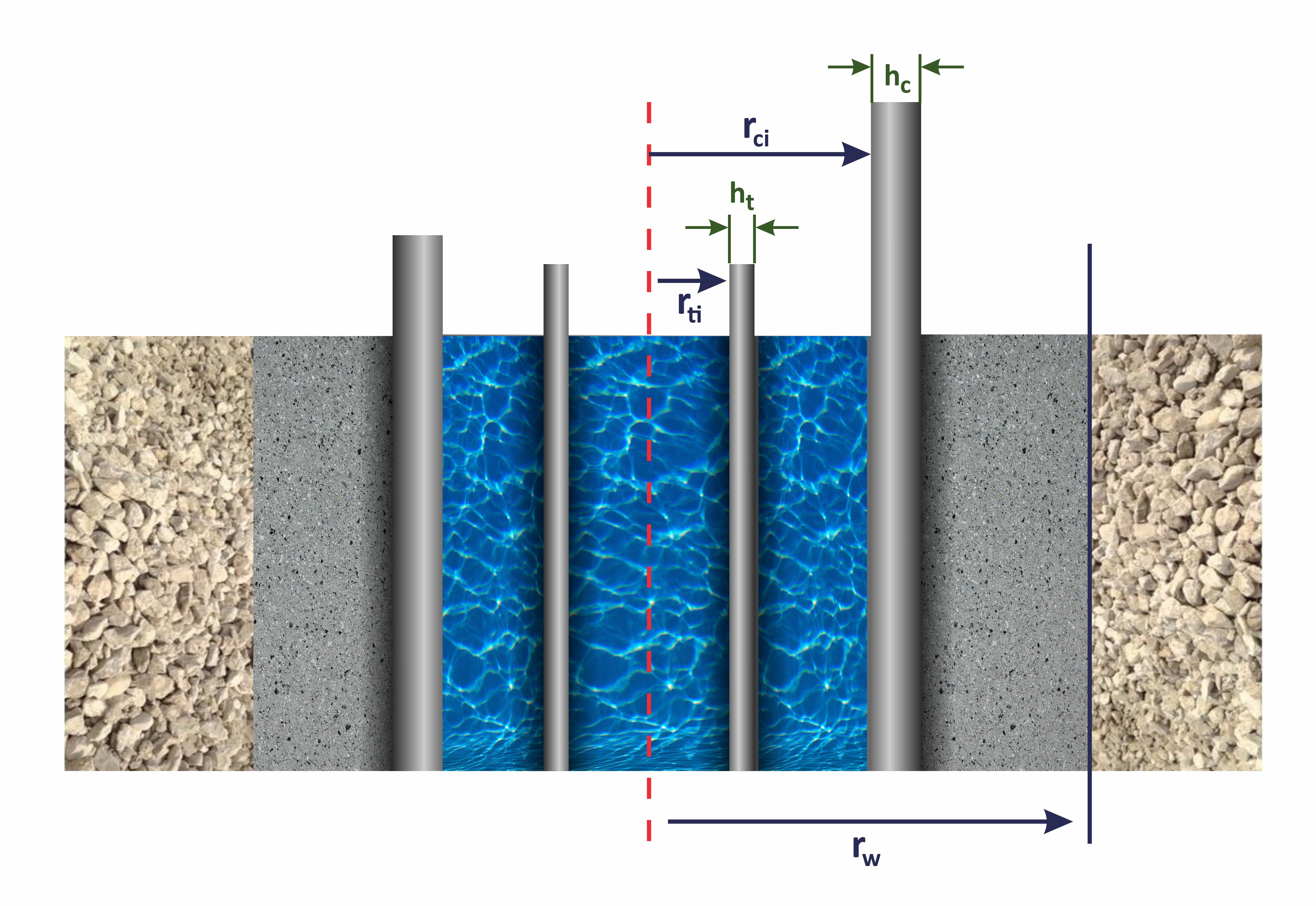
inner diameter of the tubing (with inner radius )
outer radius of casing (with outer radius )
inner diameter of the casing (with inner radius )
heat transfer coefficient (HTC)
between inner surface of tubing and moving fluid