Heat flow equation for Semispace Linear Conduction: \frac{\partial T}{\partial t} = a^2 \Delta T = a^2\frac{\partial^2 T}{\partial z^2} |
Initial Conditions Boundary conditions T(t, z=0) = T_f = {\rm const}, \quad T(t, z \rightarrow \infty) = T_G(z) |
The exact solution is given by following formula: T(t,z) = T_f + (T_G(z) - T_f) \cdot \frac{2}{\sqrt{\pi}} \int_0^{z/\sqrt{4at}} e^{-\xi^2} d\xi |
A fair approximation at late times ( ) is given by expanding the integral: ) is given by expanding the integral: T(t,z) = T_f + (T_G(z) - T_f) \cdot \Bigg[ 1- \frac{\exp(-\zeta^2)}{\sqrt{\pi} \zeta} \bigg( 1- \frac{1}{2 \zeta} + \frac{3}{4 \zeta^3} \bigg) \Bigg] |
where The final solution for temperature above the flowing unit is represented by RHK pipe flow solution where TG is replaced with Tb from  . .
For the intervals between two injection units the one needs to account for the SLC contribution from upper flowing unit and from lower flowing unit which can be done using the superposition.
First, let's rewrite  in terms of temperature gain: in terms of temperature gain: dT(t, z) = T(t,z) - T_G(z)= - (T_G(z) - T_f) \cdot \frac{\exp(-\zeta^2)}{\sqrt{\pi} \zeta} \bigg( 1- \frac{1}{2 \zeta} + \frac{3}{4 \zeta^3} \bigg) |
Now one can write down the temperature disturbance from the overlying flowing unit A1: dT_{b,over}(t, z) = T_{b,up}(t,z) - T_G(z)= - (T_G(z) - T_{f, A1}) \cdot \frac{\exp(-\zeta^2)}{\sqrt{\pi} \zeta} \bigg( 1- \frac{1}{2 \zeta} + \frac{3}{4 \zeta^3} \bigg) |
and from the underlying flowing unit A2: dT_{b,under}(t, z) = T_{b,up}(t,z) - T_G(z)= - (T_G(z) - T_{f, A2}) \cdot \frac{\exp(-\zeta^2)}{\sqrt{\pi} \zeta} \bigg( 1- \frac{1}{2 \zeta} + \frac{3}{4 \zeta^3} \bigg) |
The background temperature disturbance between the flowing units will be: T_b(t, z) = T_G(z) + dT_{b,over}(t, z) + dT_{b,under}(t, z) |
Replacing the static value of 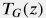 in RHK model with dynamic value of in RHK model with dynamic value of  one arrives to the final wellbore temperature model with account of heat exchange with surrounding rocks and cooling effects from flowing units (Semispace Linear Conduction). one arrives to the final wellbore temperature model with account of heat exchange with surrounding rocks and cooling effects from flowing units (Semispace Linear Conduction).
| to account for the lateral reservoir flow with a constant temperature (see Fig. 1 and Fig. 2).