Assume steady-state, incompressible, inviscid, laminar flow in a horizontal pipe (no change in elevation) with negligible frictional losses with incharge fluid velocity  and discharge velocity  at the orifice exit. The mass conservation (equivalent to continuity equation): \rho \, q = \rho \, v_{in} \, A_{in} = \rho \, v_{out} \, A_{out} \Leftrightarrow v_{in} = \frac{q}{A_{in}}, \, v_{out} = \frac{q}{A_{out}} |
where A_{in} = \frac{\pi \, D^2}{4} \, A_{out} = \frac{\pi \, d^2}{4} |
Bernoulli's equation reduces to an equation relating the conservation of energy between two points on the same streamline: p_{in} + \frac{1}{2} \rho v^2_{in} = p_{out} + \frac{1}{2} \rho v^2_{out} |
\Delta p = p_{in} - p_{out} = \frac{1}{2} \rho v^2_{out} - \frac{1}{2} \rho \, v^2_{in} = \frac{1}{2} \rho \, v^2_{out} \cdot \left[ 1 - \frac{v^2_{in}}{v^2_{out}} \right] |
\Delta p = \frac{1}{2} \rho \, \left( \frac{q}{A_{in}} \right)^2 \cdot \left[ 1 - \frac{A^2_{out}}{A^2_{in}} \right] = \frac{\rho \, q^2}{2 \, A^2_{in}} \cdot \left[ 1 - \frac{d^4}{D^4} \right] = \frac{\rho \, q^2}{2 \, A^2_{in}} \cdot \left[ 1 - \beta^4 \right] |
\Delta p = \frac{\rho \, q^2}{2 \, \left( \frac{\pi}{4} d^2 \right)^2} \cdot \left[ 1 - \beta^4 \right] = \frac{8 \, \rho \, q^2}{\pi^2 \, d^4 } \cdot \left[ 1 - \beta^4 \right] |
The above can rewritten as flowrate estimation with a given pressure drop 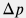 : q = \frac{\pi \, d^2}{4} \, \sqrt{\frac{2 \, \Delta p}{\rho \, (1 - \beta^4)}} |
The actual rate through the orifice with account for the choke/orifice geometry, friction and viscous forces is corrected by introducing the discharge coefficient  : q = C_d \frac{\pi \, d^2}{4} \, \sqrt{\frac{2 \, \Delta p}{\rho \, (1 - \beta^4)}} |
and correction for fluid compressibility is given by expansion factor 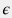 : q = \epsilon \, C_d \frac{\pi \, d^2}{4} \, \sqrt{\frac{2 \, \Delta p}{\rho \, (1 - \beta^4)}} |
|