Effective drainage radius for numerical well-reservoir contact model:
r_e = 0.28 \ \frac{ \sqrt{
\Big( \frac{k_{\perp 2}}{k_{\perp 1}} \Big)^{1/2} D_{\perp 1} ^2
+
\Big( \frac{k_{\perp 1}}{k_{\perp 2}} \Big)^{1/2} D_{\perp 2} ^2
} }
{ \Big( \frac{k_{\perp 2}}{k_{\perp 1}} \Big)^{1/4} + \Big( \frac{k_{\perp 1}}{k_{\perp 2}} \Big)^{1/4}} |
where 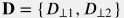 – dimensions of the grid cell around well in transversal plane to the well axis.
Strictly speaking, the above formula is only valid in case well penetrates through the whole length of grid cell 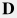 perpendicular to the cell faces. There are many modifications and generalizations of the Peaceman formula but in the most practical cases it works very well when suffucciently fine local grid refinement (LGR) is applied. |
In particular case of isotropic permeability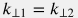 
the Peaceman effecxtive radius is given by:
r_e = 0.28 \ \sqrt{D_{\perp 1} ^2+ D_{\perp 2} ^2}
|
and in case of a square grid cell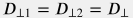 
:
Obviously, there is a natural limit to the degree of LGR for Peaceman approach.
The formula 
assumes that external boundary of drainage area is greater than well radius which introduces a natural limitation to applicability of the Peaceman formula for pressure calculations in near-reservoir zone with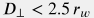 
.
This is, for example, the case in self-pulse testing where time lag between pressure responde to the flow variation is so small (seconds) that it dictates very small grid size around wellbore and Peaceman apporach can not be properly applied. Needless to say that there are various workarounds on this problem.