@wikipedia
Consider a differential volume 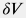 with surface area with surface area  and mass and mass  . .
Пусть в этом объеме за время  изменится масса сплошной среды за счет внешних источников (например, за счет притока флюида из ствола скважины, который вскрыл объем изменится масса сплошной среды за счет внешних источников (например, за счет притока флюида из ствола скважины, который вскрыл объем 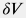 ). ).
Изменение массы  сплошной среды в этом объеме за время сплошной среды в этом объеме за время  приводит к изменению плотности среды приводит к изменению плотности среды  за то же время и притоку/оттоку флюида через поверхность объема за то же время и притоку/оттоку флюида через поверхность объема 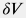 за то же время: за то же время: \frac{d \, \delta M}{dt} = \int_{\delta V} \frac{d \rho_{\delta V}}{dt} dV + \oint_{\delta \Sigma} {\bf j}_m \, dS |
где  , где , где 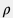 – плотность флюида, – плотность флюида, 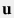 – вектор скорости потока флюида. – вектор скорости потока флюида.
В случае порового коллектора насыщенного флюидом, масса сплошной среды в объеме 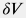 можно представить как сумму массы скелета пород можно представить как сумму массы скелета пород  и массы флюида в порах и массы флюида в порах  : :  . . В процессе фильтрации изменением плотности материала пород можно пренебречь по сравнению с изменениями плотности флюида и, следовательно, масса скелета пород в данном объеме не меняется  т. е. т. е.  . . При этом плотность среды  выражается через плотность флюида как выражается через плотность флюида как  . . Тогда закон сохранения массы среды запишется в виде: \frac{d \, \delta m}{dt} = \int_{\delta V} \frac{d (\rho \phi)}{dt} dV + \oint_{\delta \Sigma} \rho {\bf u} \, dS |
Выражая поверхностный интеграл через объемный \oint_{\delta \Sigma} \rho {\bf u} \, dS = \int_{\delta V} \nabla \cdot (\rho {\bf u}) dV |
получим закон сохранения массы в виде: \frac{d \, \delta m}{dt} = \int_{\delta V} \bigg( \frac{d (\rho \phi)}{dt} + \nabla \cdot (\rho {\bf u}) \bigg) dV |
Обозначим изменение массы флюида в выделенном объеме пласта за счет внешних источников через скорость  притока массы притока массы  и перепишем закон сохранения массы как и перепишем закон сохранения массы как
\frac{d \, \delta m}{dt} = \int_{\delta V} q_m dV = \int_{\delta V} \bigg( \frac{d (\rho \phi)}{dt} + \nabla \cdot (\rho {\bf u}) \bigg) dV |
и в силу произвольности выбора объема 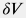 сплошной среды можно переписать закон сохранения массы в дифференциальном виде как сплошной среды можно переписать закон сохранения массы в дифференциальном виде как \frac{\partial ( \rho \phi)}{\partial t} + \nabla \cdot ({\rho \bf u}) = q_m |
и называется уравнением непрерывности сплошной среды. |