Профиль давления
В процессе эксплуатации нагнетательной скважины движение флюида вдоль ствола 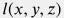 происходит в стационарном режиме, при этом профиль скорости потока происходит в стационарном режиме, при этом профиль скорости потока 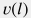 и давления и давления 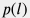 удовлетворяют удовлетворяют условию баланса массы движущегося потока: A(l) \, \rho(l) \, v(l) = \rm const |
и баланса сил действующих на единицу объема флюида в стволе скважины: \frac{dp}{dl} = \rho \, g \, \sin \theta - \rho \, v \, \frac{dv}{dl} - \frac{ f \, \rho \, v^2 \, }{2 d} |
где | длина ствола скважины, отсчитываемая вниз от поверхности | | | профиль плотности воды | | профиль угла наклона скважины к горизонту | | профиль диаметра скважины, вдоль которого идет поток | | профиль поперечного сечения ствола скважины  | | профиль коэффициента трения Дарси | | ускорение свободного падения ( = 9.87 м2/сек ) | |
|
Эти замкнутая система уравнений для стационарного распределения давления и скорости потока вдоль трубы.
Уравнение  часто в литературе записывают как разложение изменения давление вдоль ствола скважины на компоненты: часто в литературе записывают как разложение изменения давление вдоль ствола скважины на компоненты: \frac{dp}{dl} = \bigg( \frac{dp}{dl} \bigg)_g + \bigg( \frac{dp}{dl} \bigg)_v + \bigg( \frac{dp}{dl} \bigg)_f |
где
\bigg( \frac{dp}{dl} \bigg)_g = \rho \, g \, \sin \theta, |
|
гидростатическая компонента вариации давления, формируемая гравитационными силами
- в случае движения флюида вниз она имеет положительный знак и приводит к приросту давления
- в случае движения жидкости наверх эта компонента имеет отрицательный знак и приводит
к потере давления в процессе подъема жидкости
|
\bigg( \frac{dp}{dl} \bigg)_v = - \rho \, v \, \frac{dv}{dl}, |
|
кинетическая компонента вариация давления, формируемая вариацией скорости потока 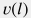 вдоль ствола скважины, которая вызвана сжатием-расжатием флюида и изменением диаметра труб вдоль ствола скважины, которая вызвана сжатием-расжатием флюида и изменением диаметра труб - в случае падения скорости потока в направлении движения она имеет положительный знак и приводит к приросту давления
- в случае роста скорости потока в направлении движения она имеет отрицательный знак и приводит к потере давления
|
\bigg( \frac{dp}{dl} \bigg)_f = - \frac{ f \, \rho v^2}{2 d}, |
|
фрикционная компонента вариации давления, формируемая трением флюида со стенкой скважины она всегда имеет отрциательный знак и приводит к потере давления вдоль направления движения потока |
Для несжимаемой жидкости  в отсутствии трения в отсутствии трения 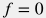 уравнение уравнение  принимает вид: принимает вид: \frac{dp}{dl} = \rho \, g \, \sin \theta - \rho \, v \, \frac{dv}{dl} |
и может быть явно проинтегрировано: p(l) - \rho \, g \, l \, \sin \theta + \frac{1}{2} \rho \, v^2 = \rm const |
и называется уравнением Бернулли.
Уравнение неразрывности одномерного потока с линейной плотностью 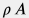 массы: массы: \frac{\partial (\rho A)}{\partial t} + \frac{\partial}{\partial l} \big( A \, \rho \, v \big) = 0 |
для стационарного режима течения принимает вид: \frac{\partial (\rho A)}{\partial t} = - \frac{\partial}{\partial l} \big( A \, \rho \, v \big) = 0 |
откуда и следует формула  . .
Для вывода уравнения  заметим, что на бесконечно малый элемент объема жидкости заметим, что на бесконечно малый элемент объема жидкости 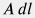 массой массой 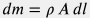 действуют четыре сил: действуют четыре сил: 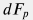 – сила гидравлического напора, вызванная разностью давлений на торцах элемента, – сила гидравлического напора, вызванная разностью давлений на торцах элемента,
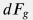 – сила гравитации, – сила гравитации,
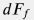 – сила трения со стенками трубы, – сила трения со стенками трубы,
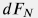 – номральная реакция опоры стенок трубы. – номральная реакция опоры стенок трубы.
Рассмотрим стационарное (то есть установившееся во времени) течение потока по трубе.
Движение поперек трубы отсуствует и, следовательно, сумма проекций всех сил на трансверсальное направление 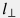 к трубе должно равняться нулю: к трубе должно равняться нулю: dF_p \bigg |_{l_{\perp}} + dF_g \bigg |_{l_{\perp}} + dF_f \bigg |_{l_{\perp}}+ dF_N \bigg |_{l_{\perp}} =0 |
и выполняется автоматически, при наличии достаточного запаса прочности трубы 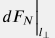 . .
Уравнение движения флюида вдоль оси трубы 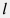 имеет вид: имеет вид:
dF_p \bigg |_l + dF_g \bigg |_l + dF_f \bigg |_l+ dF_N \bigg |_l = \frac{d I}{dt}\bigg |_l |
где 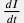 представляет собой изменение импульса представляет собой изменение импульса 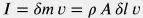 элементарного объема флюида под действием внешних сил. элементарного объема флюида под действием внешних сил.
Изменение импульса c учетом стационарности скорости потока 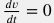 и сохранения массы и сохранения массы 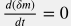 имеет вид: имеет вид: 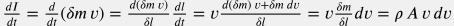 . . Сила, формируемая гидравлическим напором 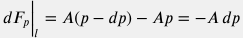 . . Проекция гравитационной силы 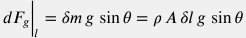 . . Сила трения со стенками трубы дается феноменологическим уравнением Дарси-Вейсбаха: 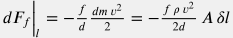 . . Аксиальная компонента реакции опоры труб по определению отсутствует 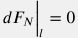 . . Подставляя вышеприведенные выражения в уравнение  получим: получим:
- A dp + \rho \, A\, \delta l \, g \, \sin \theta - \frac{f \, \rho \, v^2}{2 d} \, A \, \delta l = \rho \, A \, v \, dv
|
Разделив уравнение на бесконечно малый объем элемента 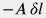 получим получим  . . |
|
Если дебит скважины на устье составляет 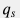 , а плотность воды на устье , а плотность воды на устье 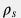 , то уравнение , то уравнение  можно записать в следующем виде: можно записать в следующем виде: A \, \rho \, v = \rho_s \, q_s |
откуда можно выразить явно профиль скорости потока по стволу: v(l) = \frac{\rho_s \, q_s}{\rho(p) \, A(l)} |
Подставляя  в в  получим уравнение на профиль давления вдоль ствола: получим уравнение на профиль давления вдоль ствола: \frac{dp}{dl} = \rho \, g \, \sin \theta - \frac{\rho_s^2 \, q_s^2}{A} \frac{d}{dl} \bigg( \frac{1}{A \, \rho} \bigg) - \frac{\rho_s^2 \, q_s^2 }{2 A^2 d} \frac{f}{\rho} |
Далее учтем, что угол наклона к горизонту 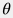 может быть выражен через абсолютные отметки глубин может быть выражен через абсолютные отметки глубин 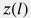 вдоль траектории скважины вдоль траектории скважины 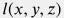 : : \sin \theta = \frac{dz}{dl} |
и уравнение для давление примет вид: \frac{dp}{dl} = \rho \, g \, \frac{dz}{dl} - \frac{\rho_s^2 \, q_s^2}{A} \frac{d}{dl} \bigg( \frac{1}{A \, \rho} \bigg) - \frac{\rho_s^2 \, q_s^2 }{2 A^2 d} \frac{f}{\rho} |
Диаметр труб, вдоль которых идет движение воды, остается постоянным на долгом протяжении и меняется редко (например, километр НКТ и потов выход потока в колонну), и это позволяет решать задачу нахождения профиля давления на кусках постоянного диаметра  и уравнение может быть переписано следующим образом: и уравнение может быть переписано следующим образом: \frac{dp}{dl} = \rho \, g \, \frac{dz}{dl} - \frac{\rho_s^2 \, q_s^2}{A^2} \frac{d}{dl} \bigg( \frac{1}{\rho} \bigg) - \frac{\rho_s^2 \, q_s^2 }{2 A^2 d} \frac{f}{\rho} |
Процесс движения воды вдоль трубы происходит в состоянии термодинамического равновесия и плотность воды является функцией только давления 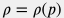 и, следовательно: и, следовательно: \frac{d}{dl} \bigg( \frac{1}{\rho} \bigg) = -\frac{1}{\rho^2} \frac{d \rho}{ dl}
= - \frac{1}{\rho^2}\frac{d \rho}{dp} \frac{dp}{ dl}
=- \frac{c}{\rho} \frac{dp}{ dl} |
где 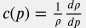 – сжимаемость воды и уравнение профиля давления принимает вид: – сжимаемость воды и уравнение профиля давления принимает вид: \bigg( 1 - \frac{c(p) \, \rho_s^2 \, q_s^2}{A^2} \bigg ) \frac{dp}{dl} = \rho(p) \, g \, \frac{dz}{dl} - \frac{\rho_s^2 \, q_s^2 }{2 A^2 d} \frac{f(p)}{\rho(p)} |
Функция 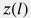 определяется траекторией скважины. определяется траекторией скважины.
Cжимаемость 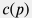 и плотность и плотность 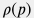 воды слабо зависят от вариации давления вдоль ствола. воды слабо зависят от вариации давления вдоль ствола. Как будет показано ниже коэффициент трения 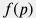 тоже слабо зависит от вариации давления и, следовательно, уравнение тоже слабо зависит от вариации давления и, следовательно, уравнение  представляет собой обыкновенное дифференциальное уравнение первого порядка на функцию представляет собой обыкновенное дифференциальное уравнение первого порядка на функцию 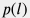 со слабой нелинейностью. со слабой нелинейностью.
Если предположить постоянство коэффициента трения 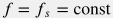 и несжимаемость флюида и несжимаемость флюида 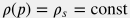 , то уравнение , то уравнение  можно явно проинтегрировать: можно явно проинтегрировать: p(l) = p_s + \rho \, g \, z(l) - \frac{\rho_s \, q_s^2 }{2 A^2 d} \, f_s \, l |
Pressure gradient will be: \frac{dp}{dl} = \rho \, g \, \cos \theta(l) - \frac{\rho_s \, q_s^2 }{2 A^2 d} \, f_s |
where 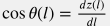 The first term defines the hydrostatic column of static fluid while the last term defines the friction losses under fluid movement: \frac{dp}{dl} \Bigg|_{loss} = \frac{\rho_s \, q_s^2 }{2 A^2 d} \, f_s |
В калькуляторе Well Flow Performance Calculator можно оценить величину потерь на трения для различных сценариев диаметров труб и дебитов скважин. Коэффициент трения
Коэффициент трения Дарси 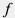 сложным образом зависит от режима течения, а также формы и шероховатости внутренних стенок трубы. сложным образом зависит от режима течения, а также формы и шероховатости внутренних стенок трубы.
Для гладкой трубы 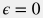 с круглым сечением коэффициент трения имеет следующие эмпирические аппроксимации: с круглым сечением коэффициент трения имеет следующие эмпирические аппроксимации: | |
ламинарный режим течения | нет стабильных корреляций | | переходной режим течение |
f = 0.32 \, \rm Re^{-0.25} |
| |
турбулентный режим течения |
f = 0.184 \, \rm Re^{-0.2} |
| |
сильно турбулентный поток режим течения |
где | число Рейнольдса | | профиль диаметра трубы, вдоль которой движется поток | | профиль вязкости флюида, определяемая зависимостью вязкости от давления и температуры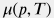 в состоянии термодинамического равновесия в состоянии термодинамического равновесия |
Для переходных и турбулентных режимов течения коэффициент трения удовлетворяет эмпирической модели Колбрука-Уайта (Colebrook–White), которая учитывает шероховатость внутренней поверхности трубы
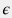 (в мм) (в мм) \frac{1}{\sqrt{f}} = -2 \, \log \Bigg( \frac{\epsilon}{3.7 \, d} + \frac{2.51}{{\rm Re} \sqrt{f}} \Bigg) |
Типичное значение шероховатости труб 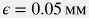 , однако по мере эрозийного воздействия потока и отложения минеральных осадков шероховатость может подняться в разы. , однако по мере эрозийного воздействия потока и отложения минеральных осадков шероховатость может подняться в разы.
Существует множество явных аппроксимаций решения уравнения  , в частности следующая (Monzon, Romeo, Royo, 2002): , в частности следующая (Monzon, Romeo, Royo, 2002): f = 0.25 \, \bigg[ \log \bigg( \frac{\epsilon / d}{3.7065} - \frac{5.0272}{\rm Re} \log \Lambda \bigg) \bigg]^{-2} |
где 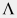 – безразмерный параметр, рассчитываемый по формуле: – безразмерный параметр, рассчитываемый по формуле: \Lambda = \frac{(\epsilon/d)}{3.827} - \frac{4.657}{\rm Re} \log \Bigg[ \bigg( \frac{\epsilon/d}{7.7918} \bigg)^{0.9924} + \bigg( \frac{5.3326}{208.815+Re} \bigg)^{0.9345} \Bigg] |
Однако, в пределах измерительной погрешности (< 2 %) можно пользоваться универсальной корреляцией (Churchil) для всех режимов течения, от ламинарного до сильно турбулентного: f = \frac{64}{\rm Re} \, \Bigg [ 1+ \frac{\big(\rm Re / 8 \big)^{12} }{ \big( \Theta_1 + \Theta_2 \big)^{1.5} } \Bigg]^{1/12} |
где 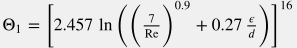 и и 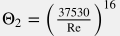 . .
Как видно из вышеприведенных корреляций, коэффициент трения меняется в зависимости от скорости потока и соответствующего числа Рейнольдса. Основным вкладом в вариабельность коэффициента трения вдоль трубы является диаметр трубы в данной точке траектории скважины, который может приводить к значительным изменениям скорости потока. Тем не менее, зависимость от дебита является слабой. Из формулы  видно что изменение дебит в 10 раз приводит к изменению коэффициента трения в видно что изменение дебит в 10 раз приводит к изменению коэффициента трения в 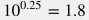 раз. раз.
Еще более слабой является вариабельность коэффициента трения от давления вдоль ствола, что можно проиллюстрировать следующими соображениями.
Зависимость коэффициента трения от давления формируется только через число Рейнольдса: 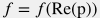 . .
При этом число Рейнольдса 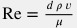 с учетом с учетом  можно записать как: можно записать как:
{\rm Re} = \frac{ d \, \rho_s \, q_s}{A \, \mu(p)} |
отсюда следует, что зависимость коэффициента трения от давления формируется вязкостью 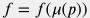 , которая для воды имеет слабую зависисмость от давления в широких практических пределах: , которая для воды имеет слабую зависисмость от давления в широких практических пределах:
δμ/μ = 25 % при вариации μ = 2.4·10-5 Па · с для p = 1 атм до μ = 3.0·10-5 Па · с для 300 атм (cм. Свойства воды).
Это приводит к 25 % вариации коэффициента трения для ламинарного потока (в котором сила трения минимальна) и порядка 4.5 % для турбулентного потока (и максимальным вкладом трения).
Для оценки числа Рейнольдса для нагнетаемой по 2.5 " НКТ воды можно пользоваться формулой 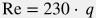 , где , где 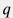 дебит скважины на устье в м3/сут. дебит скважины на устье в м3/сут. Отсюда видно, что при дебитах более 18 м3/сут число Рейнольдса становится больше 4,000 и режим течения является турбулентным и коэффициент трения можно считать практически постоянным вдоль ствола нагнетательной скважины.
А учитывая, что рост давления с глубиной сопровождается увеличением температуры, что компенсирует рост вязкости воды, то для большинства практических реализаций ППД можно полагать, что вариация коэффициента трения вдоль ствола не превышает 2-3 % и в оценках потери напора на трение принимать коэффициент трения постоянным 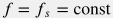 . .
Профиль температуры
В отличие от задач гидравлики процессы теплообмена существенно нестационарны и температурный профиль жидкости и окружающих скважину пород будет непрерывно меняться в процессе закачки. Хотя со временем изменения могут становиться настолько малы, что ими можно пренебречь в пределах погрешности измерительной аппаратуры в пределах времени конкретного исследования скважины. В этом случае говорят о квазистационарном распределении температурного поля. Помимо этого процесс распространения тепла идет не только в стволе скважины, где распространяется поток, но и далеко за ее пределами, что приводит к необходимости решать задачу и температурном поле скважины в совокупности с прилегающими к ней породами, что увиливает размерность задачи с одномерной до трехмерной (или двухмерной в случае осевой симметрии теплофизических параметров пород).
Поэтому решение задачи термометрии в стволах скважины формулируется на две температурные функции: | температурный профиль потока воды вдоль ствола скважины 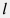 , отсчитываемой вниз от поверхности , отсчитываемой вниз от поверхности | | распределение температуры в массиве горных пород 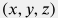 |
Температурный профиль 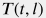 потока воды ствола скважины формируется кондукцией и конвекцией вдоль потока и теплообменом с окружающими породами и описывается следующим уравнением: потока воды ствола скважины формируется кондукцией и конвекцией вдоль потока и теплообменом с окружающими породами и описывается следующим уравнением: \rho \, c \, \frac{\partial T}{\partial t} = \frac{d}{dl} \, \bigg( \lambda \, \frac{dT}{dl} \bigg) - \rho \, c \, v \, \frac{dT}{dl} |
с начальным условием: и граничным условием на поверхности:
Распределение температуры в массиве горных пород 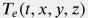 формируется кондукцией горных породах и теплообменом со стволом скважины и описывается следующим уравнением: формируется кондукцией горных породах и теплообменом со стволом скважины и описывается следующим уравнением:
\rho_e \, c_e \, \frac{\partial T_e}{\partial t} = \nabla ( \lambda_e \nabla T_e) |
с начальным условием: и граничным условием на бесконечном удалении от скважины: T_e(t, l, r \rightarrow \infty) = T_g(l) |
Геотермическое распределение температуры (также называемое геотермой) вдоль ствола скважины 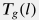 задается следующей моделью задается следующей моделью T_g(l) = T_{0e} + \int_{z_0}^{z(l)} G_T(z) dz = T_{0e} + \int_{l_0}^l G_T(z(l)) \sin \theta dl |
геотермический градиент задается отношением регионального теплового потока из недр Земли 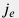 и теплопроводностью пород и теплопроводностью пород 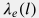 G_T(z(l)) = \frac{j_e}{\lambda_e(l)} |
где | величина регионального теплового потока из недр Земли (см. также Геотермия) | | профиль теплопроводности пород вдоль траектории скважины | | абсолютная отметка глубины залегания нейтрального слоя (обычно единицы ) | | отметка нейтрального слоя вдоль траектории скважины (обычно 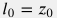 так как начальные участки скважин не имеют сильного отклонения от вертикали) так как начальные участки скважин не имеют сильного отклонения от вертикали) |
В регионах, где геотермический градиент остается постоянным 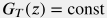 до глубины залегания продуктивных пластов, геотермическое распределение температуры в породах принимает простой вид: до глубины залегания продуктивных пластов, геотермическое распределение температуры в породах принимает простой вид: T_g(l) = T_{0e} + G_T \, z |
Однако в большом количестве практических случаев это не так и применение среднего по всему разрезу значения геотермического градиента для оценки геотермического распределения температур по формуле  может привести к значительным погрешностям. может привести к значительным погрешностям. Справедливости ради стоит заметить, что эта проблема становится актуальной при анализе термограмма в бурящих и добывающих скважинах, а при анализе водяных нагнетательных скважин, использование постоянного усредненного термоградиента вполне допустимо.
Замыкает систему уравнений условие теплобмена между жидкостью в стволе скважины и окружающими горными породами, задаваемое условием непрерывности радиального теплового потока: 2 \pi \, \lambda_e \, r_w \, \frac{\partial T_e}{\partial r} \, \bigg|_{r=r_w} = 2 \pi \, r_f \, U \, \bigg( T_e \, \bigg|_{r=r_w} - T \bigg) |
где 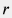 – радиальное направление к оси скважины. – радиальное направление к оси скважины.
Если между внутренней стенкой НКТ и внутренней стенкой скважины по долоту нет источников или стоков тепла, то линейная плотность радиального потока тепла 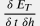 (количество тепла переносимого вдоль радиального направления в единицу времени на метр длины скважины) будет сохраняться вдоль радиального направления. (количество тепла переносимого вдоль радиального направления в единицу времени на метр длины скважины) будет сохраняться вдоль радиального направления. Плотность радиального теплового потока между закачиваемой жидкостью и стенкой трубки НКТ может быть выражена через коэффициент теплопередачи 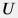 между средами: между средами: j = \frac{\delta \, E_T}{\delta \, t \: \delta S_f } = \frac{\delta \, E_T}{\delta \, t \: \delta h \: 2 \pi \, r_f } = U \, \bigg( T_e \, \bigg|_{r=r_w} - T \bigg) |
Это по-сути эта формула является определением коэффициента теплопередачи. Плотность радиального теплового потока между стенкой скважины и породами определяется законом теплопроводности Фурье: j = \frac{\delta \, E_T}{\delta \, t \: \delta S_w } = \frac{\delta \, E_T}{\delta \, t \: \delta h \: 2 \pi \, r_w } = \lambda \, \frac{\partial T}{\partial r} |
Исключая из вышеприведенных уравнений линейную плотность теплового потока 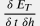 получим условие теплообмена получим условие теплообмена  . . |
Эта задача решается численными методами. Но для простых случаев есть аналитические оценки, которые правильно воспроизводят крупномасштабные формы температурного профиля. Одна из популярных аналитических моделей для стационарной (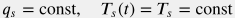 ) закачки в скважину с постоянным наклоном ( ) закачки в скважину с постоянным наклоном (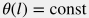 ), в окружении акисально-симметричного однородного пласта ), в окружении акисально-симметричного однородного пласта (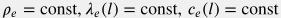 ) с постоянным геотермическим градиентом ) с постоянным геотермическим градиентом 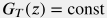 вдали от поверхности вдали от поверхности 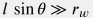 , дается следующей формулой (Ramey, 1962): , дается следующей формулой (Ramey, 1962): T(t, l) = T_{0e} + G_T \, z - R(t) \, G_T \, \sin \theta + \big( T_s - T_{0e} + R(t) \, G_T \, \sin \theta \big) \, e^{ - l/R(t)} |
где
R(t) = \frac{q_s}{2 \pi \, a_e} \, \bigg( T_D(t) + \frac{\lambda_e}{r_f \, U} \bigg) |
|
релаксационное расстояние |
T_D(t) = \ln \big[ e^{-0.2 \, t_D} + (1.5 - 0.3719 \, e^{-t_D}) \, \sqrt{t_D} \big] |
|
безразмерная температура (Hasan, Kabir, 1994) |
t_D(t) = \frac{a_e \, t}{r_w^2} |
|
безразмерное время |
a_e = \frac{\lambda_e}{ c_e \, \rho_e} |
|
температуропроводность пород | | теплопроводность пород | | объемная теплопроводжность пород при постоянном давлении | | плотность пород | | температура закачиваемого флюида на поверхности | | радиус трубы вдоль контрой идет движение флюида | | радиус скважины по долоту | | геотермический градиент невозмущенных пород | | дебит скважины на устье | | плотность закачиваемого флюида | | коэффициент теплопередачи между закачиваемым флюидом и породами |
|
предсказывает малое значение
и следовательно в экспоненте формулы
можно удержать только линейный член разложения по
:
, что соответствует практическим наблюдениям.
предсказывает большое значение
и следовательно экспонентой в формуле
можно пренебречь:
предсказывает логарифмический рост
со временем:
, то есть температура в стволе скважины перестает зависеть от радиуса НКТ и значения коэффициента теплопередачи, что тоже соответствует практическим наблюдениям.
работает в широких пределах дебетов и имеет правильные асимптоты и вполне пригодна для различного рода оценок.