Центральной задачей МРСТ как правило является нахождение базовых параметров диффузионной модели: пластовое давление 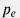 , скин-фактор , скин-фактор 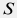 , гидропроводность , гидропроводность 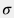 и пьезопроводность и пьезопроводность 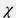 . . Но в ряде случаев, когда часть базовых параметров заранее известна, то МРСТ помогает оценить специфические параметры диффузионной модели, такие как длину трещины, эффективную длину горизонтального ствола, тип границы и т.д. Двухрежимный Стационарный Степ-Тест (2ССТ)
Двухрежимный стационарный тест представляет собой замер забойного давления на двух режимах работы скважины с постоянными дебитами  и и  (см. рис. 1) с достаточно длительным временем работы на каждом режиме, которые обеспечивают выход на стабилизированный режим эксплуатации, характеризующийся постоянной (или примерно постоянной) продуктивностью (см. рис. 1) с достаточно длительным временем работы на каждом режиме, которые обеспечивают выход на стабилизированный режим эксплуатации, характеризующийся постоянной (или примерно постоянной) продуктивностью 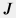 : : J = \frac{q_{t1}}{p_e - p_{wf1}} = \frac{q_{t2}}{p_e - p_{wf2}} |
При этом тест должен быть достаточно коротким, чтобы пластовое давление за время теста не успело сильно измениться: p_e = p_e(\Delta t_1) = p_e(\Delta t_2) |
Замер забойного давления производится в конце каждого режима и разница в показаниях  будет отражает реакцию пласта на смену режима эксплуатации с будет отражает реакцию пласта на смену режима эксплуатации с  на на  (см. рис. 1). (см. рис. 1).
| | Рис 1. Схема двух-режимного стационарного теста (2ССТ) |
Выбор времени работы на каждом режиме является критическим элементом планирования теста и может осуществляться как за счет практических наблюдений по данному месторождению, так и методами диффузионного анализа (СГДИ - Односкважинные ГДИ), если проводились соотвествующие тесты.
Результатом интерпретации является оценка текущего пластового давления на контуре питания: p_e = \frac{q_{t1} p_{wf2} - q_{t2} p_{wf1}}{q_{t1} - q_{t2}} |
и значение продуктивности на момент проведения теста: J = \frac{q_{t1} - q_{t2}}{p_{wf2} - p_{wf1}} |
Этот тест является полезным для случаев, когда возможности измерения давления в скважине ограничены. Этот тест требует всего два замера давления в конце каждого режима. Двухрежимный Нестационарный Степ-Тест (2НСТ)
Двухрежимный стационарный тест представляет собой непрерывную запись забойного давления 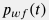 от времени после смены режима работы скважины с от времени после смены режима работы скважины с  на на  ( см. рис. 2). ( см. рис. 2). | | Рис 2. Схема двух-режимного нестационарного теста (2НСТ) - исправить рисунок |
Обозначим время работы скважины на предыдущем режиме через 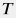 и привяжем отсчет времени и привяжем отсчет времени 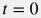 к смене режима с к смене режима с  на на  . . Тогда забойное давление на момент смены режима может быть представлено как (см.  ): ): p_{wf}(t=0) = p_e + \frac{q_{t1}}{4 \pi \sigma} \, \bigg[ - 2S + F \bigg( - \frac{r_w^2}{4 \chi T} \bigg) \bigg] |
Смена дебита с  на на  для линейных режимов диффузии может быть представлена (в силу справедливости принципа суперпозиции во времени) как запуск в момент времени для линейных режимов диффузии может быть представлена (в силу справедливости принципа суперпозиции во времени) как запуск в момент времени 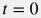 второй скважины с дебитом второй скважины с дебитом  : : p_{wf}(t) = p_e + \frac{q_{t1}}{4 \pi \sigma} \, \bigg[ - 2S + F \bigg( - \frac{r_w^2}{4 \chi (T + t)} \bigg) \bigg] + \frac{q_{t2}-q_{t1}}{4 \pi \sigma} \, \bigg[ - 2S + F \bigg( - \frac{r_w^2}{4 \chi t} \bigg) \bigg] |
или p_{wf}(t) = p_e + \frac{q_{t1}}{4 \pi \sigma} \, \bigg[ F \bigg( - \frac{r_w^2}{4 \chi (T+t)} \bigg) - F \bigg( - \frac{r_w^2}{4 \chi t} \bigg) \bigg] + \frac{q_{t2}}{4 \pi \sigma} \, \bigg[ - 2S + F \bigg( - \frac{r_w^2}{4 \chi t} \bigg) \bigg] |
Здесь предполагается, что скин-фактор на обоих режимах одинаковый, хотя на практике встречаются ситуации, когда скин-фактор зависит от приложенной депрессии (см.  ) и для них нижеприведенные методы экспресс-анализа неприменимы. ) и для них нижеприведенные методы экспресс-анализа неприменимы.
Отсюда несложными преобразованиями можно получить следующую форму уравнений: p_e = p_{wf}(0) - \frac{q_{t1}}{4 \pi \sigma} \, \bigg[ - 2S + F \bigg( - \frac{r_w^2}{4 \chi T} \bigg) \bigg] |
4 \pi \sigma ( p_{wf}(0) - p_{wf}(t) ) = 2S(q_{t1}-q_{t2})
- q_{t1} \, F \bigg( - \frac{r_w^2}{4 \chi (T+t)} \bigg)
+ q_{t2} \, F \bigg( - \frac{r_w^2}{4 \chi t} \bigg) |
Уравнение  является расчетной формулой для пластового давления является расчетной формулой для пластового давления 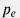 , когда все остальные параметры диффузионной модели определены. , когда все остальные параметры диффузионной модели определены. Уравнение  связывает отклик давления на смену режима работы скважины с параметрами скважины и пласта. связывает отклик давления на смену режима работы скважины с параметрами скважины и пласта. Структура функции  такова, что они медленно зависят от аргумента (как правило логарифмически), и, следовательно, разность забойных давлений после смены режима в меньшей степени зависит от неточностей в оценке пьезопроводности такова, что они медленно зависят от аргумента (как правило логарифмически), и, следовательно, разность забойных давлений после смены режима в меньшей степени зависит от неточностей в оценке пьезопроводности 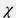 (по сравнению с влиянием скин-фактора (по сравнению с влиянием скин-фактора 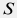 и гидропроводности и гидропроводности 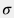 , которое весьма велико) и которую можно рассчитать по усредненным данным РИГИС и весьма приближенной оценке текущей насыщенности пласта (см. , которое весьма велико) и которую можно рассчитать по усредненным данным РИГИС и весьма приближенной оценке текущей насыщенности пласта (см.  ). ). Тогда уравнение  можно переписать как можно переписать как \frac{q_{t1}}{q_{t1}-q_{t2}} \, F \bigg( - \frac{r_w^2}{4 \chi (T+t)} \bigg)
- \frac{q_{t2}}{q_{t1}-q_{t2}} \, F \bigg( - \frac{r_w^2}{4 \chi t} \bigg)
= \frac{4 \pi \sigma}{q_{t1}-q_{t2}} \big( p_{wf}(t) - p_{wf}(0) \big) + 2S
|
и произвести простую МНК-регрессию между временными функциями  и и  , откуда находятся коэффициенты регрессии , откуда находятся коэффициенты регрессии  и и  , а следовательно скин-фактор , а следовательно скин-фактор 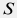 и гидропроводность и гидропроводность 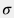 . После чего можно определить пластовое давление . После чего можно определить пластовое давление 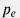 по формуле по формуле  . . Этот тест весьма популярен при исследованиях транзиента после останова скважины, которая к моменту исследования находилась в длительной эксплуатации с постоянным (или почти постоянным) дебитом. Под "длительной" понимается время, превыщающее время самого исследования после останова:  . . Это условие, по-сути, обеспечивает затухание вклада от ее истории в ранние времена  и помогает производить корректную интерпретацию даже если история скважины до момента времени и помогает производить корректную интерпретацию даже если история скважины до момента времени  была неизвестна, либо не была достоверной. была неизвестна, либо не была достоверной. Однако на практике выбор очень длинных 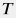 также не рекомендуется, если скважина не является одиночной на участке. также не рекомендуется, если скважина не является одиночной на участке. За длительное время она неизбежно вступает в интерференцию с соседними скважинами, динамика давления подвергается влиянию соседей и интерпретация показаний давления на основе односквжаинной диффузионной модели может привезти к ошибочным результатам. С логистической точки зрения, полевому инженеру необходимо прибыть на устье скважины, спустить манометр в работающей скважине, произвести остановку скважины и по истечении запланированного времени достать прибор на поверхность. Если же скважина оборудована перманентным датчиком давления, то необходимо остановить скважину на время 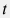 , чем период предыдущей работы скважины с постоянным дебитом и проинтепрпретировать динамику давления после останова вышеуказанным методом. , чем период предыдущей работы скважины с постоянным дебитом и проинтепрпретировать динамику давления после останова вышеуказанным методом.
Хорнер тест Тест Хорнера относится к частному случаю двухрежимного нестационарного теста (2НТ), при котором скважину после длительной эксплуатации с постоянным дебитом  в течении времени в течении времени 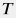 отключают и регистрируют динамику забойного давления отключают и регистрируют динамику забойного давления 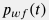 , где отсечет времени , где отсечет времени 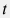 ведется с момента остановки скважины. То есть по сути это это 2НТ с ведется с момента остановки скважины. То есть по сути это это 2НТ с  (см. рисунок 3). (см. рисунок 3).
| | Рис 3. Схема Хорнер-теста - исправить рисунок |
Из формулы  при при  следует: следует: p_{wf}(t) = p_e - \frac{q_t}{4 \pi \sigma} \, \bigg[ F \bigg( - \frac{r_w^2}{4 \chi (t - T)} \bigg) - F \bigg( - \frac{r_w^2}{4 \chi t} \bigg) \bigg] |
Отсюда следует что транзиент давления на остановке не содержит сведения о скин-факторе. Если однородный пласт полностью вскрыт вертикальной скважиной без трещин и на временах порядка времени наблюдения 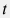 граница не достигается, то диффузия происходит в режиме IARF и граница не достигается, то диффузия происходит в режиме IARF и  , откуда: , откуда: p_{wf}(t) = p_e - \frac{q_t}{4 \pi \sigma} \, \bigg[ \gamma + \ln \bigg( - \frac{r_w^2}{4 \chi (t - T)} \bigg) - \gamma - \ln \bigg( - \frac{r_w^2}{4 \chi t} \bigg) \bigg] = p_e - \frac{q_t}{4 \pi \sigma} \, \ln \frac{t}{t-T} |
Отсюда видно, что в этом режиме течения влияние пьезопроводности на динамику давления Хорнер-теста полностью отсутствует и с помощью простого  в координатах в координатах  легко находится пластовое давление на начало теста легко находится пластовое давление на начало теста 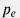 и гидропроводность пласта и гидропроводность пласта 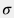 . . Хорнер-тест является ярким примером того, как мультирежимный тест позволяет свести сложную задачу анализа транзиента и неоднозначного поиска в трехмерном пространстве  к последовательности простых прямых вычислительных процедур с однозначным результатом. к последовательности простых прямых вычислительных процедур с однозначным результатом.
Трехрежимный нестационарный тест (3НТ)
| | Рис 4. Схема трех-режимного нестационарного теста (3НТ) |
\begin{cases}
p_{wf1} = p_i + \frac{q_1 B}{4\pi \sigma}[-2S + \gamma + \ln{\frac{r^2_w}{4 \chi \Delta t_1}}] \\
p_{wf2} = p_i + \frac{q_1 B}{4\pi\sigma}[-2S + \gamma +\ln{\frac{r^2_w}{4\chi(\Delta t_1 + \Delta t_2)}}] + \frac{(q_2 - q_1)B}{4 \pi\sigma} [-2S + \gamma + \ln{\frac{r^2_w}{4\chi\Delta t_2}}] \\
p_{wf3} = p_i + \frac{q_1 B}{4 \pi \sigma}[-2S + \gamma + \ln{\frac{r^2_w}{4\chi (\Delta t_1 + \Delta t_2 + \Delta t_3)}}] + \frac{(q_2 - q_1)B}{4\pi\sigma}[-2S + \gamma + \ln{\frac{r^2_w}{4\chi(\Delta t_2 + \Delta t_3)}}] + \frac{(q_3 - q_2)B}{4\pi\sigma}[-2S + \gamma + \ln{\frac{r^2_w}{4\chi\Delta t_3}}]
\end{cases}
|
|