Для модели движения летучей нефти в пласте  –  положим температуру постоянной во времени и раскроем производные по времени: T(t, \mathbf{r} ) = T = const |
и раскроем производные по времени:
s_w \partial_t \bigg ( \frac{\phi}{B_w} \bigg ) + \frac{\phi}{B_w} \partial_t s_w
+ \nabla \bigg ( \frac{1}{B_w} \ \mathbf{u}_w \bigg ) = q_W(\mathbf{r}) |
s_o \partial_t \bigg ( \frac{\phi}{B_o} \bigg ) + s_g \partial_t \bigg ( \frac{\phi \ R_v }{B_g} \bigg )
+ \bigg ( \frac{\phi}{B_o} \bigg ) \partial_t s_o + \bigg ( \frac{\phi \ R_v }{B_g} \bigg ) \partial_t s_g
+ \nabla \bigg ( \frac{1}{B_o} \ \mathbf{u}_o
+ \frac{R_v}{B_g} \ \mathbf{u}_g \bigg ) = q_O(\mathbf{r}) |
s_g \partial_t \bigg ( \frac{\phi}{B_g} \bigg ) + s_o \partial_t \bigg ( \frac{\phi \ R_s}{B_o} \bigg )
+ \bigg ( \frac{\phi}{B_g} \bigg ) \partial_t s_g + \bigg ( \frac{\phi \ R_s}{B_o} \bigg ) \partial_t s_o
+ \nabla \bigg ( \frac{1}{B_g} \ \mathbf{u}_g
+ \frac{R_s}{B_o} \ \mathbf{u}_o \bigg ) = q_G(\mathbf{r}) |
|
\mathbf{u}_w = - \alpha_w \ ( \nabla P_w - \rho_w \ \mathbf{g} ) |
\mathbf{u}_o = - \alpha_o \ ( \nabla P_o - \rho_o \ \mathbf{g} ) |
\mathbf{u}_g = - \alpha_g \ ( \nabla P_g - \rho_g \ \mathbf{g} ) |
|
|
где
\alpha_w = k_a \ \frac{k_{rw}(s_w, s_g)}{\mu_w} |
|
\alpha_o = k_a \ \frac{k_{ro}(s_w, s_g)}{\mu_o} |
|
\alpha_g = k_a \ \frac{k_{rg}(s_w, s_g)}{\mu_g} |
|
|
Учитывая, что пористость и PVT параметры явно не зависят от времени, но являются функциями от текущего давления компоненты в данной точке пласта:
s_w \bigg ( \frac{\phi}{B_w}\bigg )^{\LARGE \cdot} \partial_t P_w + \frac{\phi}{B_w} \partial_t s_w
+ \nabla \cdot \bigg ( \frac{1}{B_w} \ \mathbf{u}_w \bigg ) = q_W(\mathbf{r}) |
s_o \bigg ( \frac{\phi}{B_o} \bigg )^{\LARGE \cdot} \partial_t P_o + s_g \bigg ( \frac{\phi \ R_v }{B_g} \bigg )^{\LARGE \cdot} \partial_t P_g
+ \bigg ( \frac{\phi}{B_o} \bigg ) \partial_t s_o + \bigg ( \frac{\phi \ R_v }{B_g} \bigg ) \partial_t s_g
+ \nabla \bigg ( \frac{1}{B_o} \ \mathbf{u}_o + \frac{R_v}{B_g} \ \mathbf{u}_g \bigg ) = q_O(\mathbf{r}) |
s_g \bigg ( \frac{\phi}{B_g} \bigg )^{\LARGE \cdot} \partial_t P_g + s_o \bigg ( \frac{\phi \ R_s}{B_o} \bigg )^{\LARGE \cdot} \partial_t P_o
+ \bigg ( \frac{\phi}{B_g} \bigg ) \partial_t s_g + \bigg ( \frac{\phi \ R_s}{B_o} \bigg ) \partial_t s_o
+ \nabla \bigg ( \frac{1}{B_g} \ \mathbf{u}_g + \frac{R_s}{B_o} \ \mathbf{u}_o \bigg ) = q_G(\mathbf{r}) |
где точка означает производную по давлению \bigg ( \bigg )^{\LARGE \cdot} = \frac{d}{dP} \bigg ( \bigg ) |
Прямое вычисление дает:
\bigg ( \frac{\phi}{B_w} \bigg )^{\LARGE \cdot} = \frac{\phi}{B_w} (c_r + c_w) |
\bigg ( \frac{\phi \ R_v}{B_g} \bigg )^{\LARGE \cdot} = \frac{\phi}{B_g} ( \dot R_v + (c_r + c_g) \ R_v) |
|
\bigg ( \frac{\phi}{B_o} \bigg )^{\LARGE \cdot} = \frac{\phi}{B_o} (c_r + c_o) |
\bigg ( \frac{\phi \ R_s}{B_o} \bigg )^{\LARGE \cdot} = \frac{\phi}{B_o} (\dot R_s + (c_r + c_o) \ R_v) |
|
\bigg ( \frac{\phi}{B_g} \bigg )^{\LARGE \cdot} = \frac{\phi}{B_g} (c_r + c_g) |
|
|
и соответственно \frac{\phi}{B_w} s_w (c_r + c_w) \ \partial_t P_w + \frac{\phi}{B_w} \partial_t s_w
+ \nabla \cdot \bigg ( \frac{1}{B_w} \ \mathbf{u}_w \bigg ) = q_W(\mathbf{r}) |
\frac{\phi}{B_o} s_o (c_r + c_o) \ \partial_t P_o + \frac{\phi }{B_g} s_g \big( \dot R_v + (c_r + c_w) R_v \big) \ \partial_t P_g
+ \bigg ( \frac{\phi}{B_o} \bigg ) \partial_t s_o + \bigg ( \frac{\phi \ R_v }{B_g} \bigg ) \partial_t s_g
+ \nabla \bigg ( \frac{1}{B_o} \ \mathbf{u}_o + \frac{R_v}{B_g} \ \mathbf{u}_g \bigg ) = q_O(\mathbf{r}) |
\frac{\phi}{B_g} s_g (c_r + c_g) \ \partial_t P_g + \frac{\phi}{B_o} s_o \big( \dot R_s + (c_r + c_o) R_s \big) \ \partial_t P_o
+ \bigg ( \frac{\phi}{B_g} \bigg ) \partial_t s_g + \bigg ( \frac{\phi \ R_s}{B_o} \bigg ) \partial_t s_o
+ \nabla \bigg ( \frac{1}{B_g} \ \mathbf{u}_g + \frac{R_s}{B_o} \ \mathbf{u}_o \bigg ) = q_G(\mathbf{r}) |
Домножая обе части всех уравнений непрерывности на соотвествующий объемный коэффициент, получим: \phi \big[ c_r s_w + c_w s_w \big] \partial_t P_w + \phi \partial_t s_w
+ B_w \nabla \cdot \bigg ( \frac{1}{B_w} \ \mathbf{u}_w \bigg ) = B_w \ q_W(\mathbf{r}) |
\phi \big[ c_r s_o + c_o s_o \big] \partial_t P_o + \phi \big[ \frac{B_o \ \dot R_v}{B_g} s_g + \frac{B_o R_v}{B_g} (c_r s_g + c_g s_g) \big] \partial_t P_g
+ \phi \partial_t s_o + \big( \frac{\phi B_o R_v }{B_g} \big) \partial_t s_g
+ B_o \nabla \bigg ( \frac{1}{B_o} \ \mathbf{u}_o + \frac{R_v}{B_g} \ \mathbf{u}_g \bigg ) = B_o \ q_O(\mathbf{r}) |
\phi \big[ c_r s_g + c_g s_g \big] \partial_t P_g + \phi \big[ \frac{B_g \ \dot R_s}{B_o} s_o + \frac{B_g R_s}{B_o} (c_r s_o + c_o s_o) \big] \partial_t P_o
+ \phi \partial_t s_g + \big( \frac{\phi B_g R_s}{B_o} \big) \partial_t s_o
+ B_g \nabla \bigg ( \frac{1}{B_g} \ \mathbf{u}_g + \frac{R_s}{B_o} \ \mathbf{u}_o \bigg ) = B_g \ q_G(\mathbf{r}) |
Учтем, что B_w \ q_W = q_w \, - \, \textrm{объемный дебит водяной компоненты в пластовых условиях} |
B_o \ q_O = B_o \bigg( \frac{q_o}{B_o} + \frac{R_v q_g}{B_g} \bigg) = q_o + \frac{R_v B_o}{B_g} q_g \, - \, \textrm{объемный дебит нефтяной компоненты в пластовых условиях} |
B_g \ q_G = B_g \bigg( \frac{q_g}{B_g} + \frac{R_s q_o}{B_o} \bigg) = q_g + \frac{R_s B_g}{B_o} q_o \, - \, \textrm{объемный дебит газовой компоненты в пластовых условиях} |
и следовательно: \phi \big[ c_r s_w + c_w s_w \big] \partial_t P_w + \phi \partial_t s_w
+ B_w \nabla \cdot \bigg ( \frac{1}{B_w} \ \mathbf{u}_w \bigg ) = q_w(\mathbf{r}) |
\phi \big[ c_r s_o + c_o s_o \big] \partial_t P_o + \phi \big[ \frac{B_o \ \dot R_v}{B_g} s_g + \frac{B_o R_v}{B_g} (c_r s_g + c_g s_g) \big] \partial_t P_g
+ \phi \partial_t s_o + \big( \frac{\phi B_o R_v }{B_g} \big) \partial_t s_g
+ B_o \nabla \bigg ( \frac{1}{B_o} \ \mathbf{u}_o + \frac{R_v}{B_g} \ \mathbf{u}_g \bigg ) = \bigg( q_o(\mathbf{r}) + \frac{R_v B_o}{B_g} q_g(\mathbf{r}) \bigg) |
\phi \big[ c_r s_g + c_g s_g \big] \partial_t P_g + \phi \big[ \frac{B_g \ \dot R_s}{B_o} s_o + \frac{B_g R_s}{B_o} (c_r s_o + c_o s_o) \big] \partial_t P_o
+ \phi \partial_t s_g + \big( \frac{\phi B_g R_s}{B_o} \big) \partial_t s_o
+ B_g \nabla \bigg ( \frac{1}{B_g} \ \mathbf{u}_g + \frac{R_s}{B_o} \ \mathbf{u}_o \bigg ) = \bigg( q_g(\mathbf{r}) + \frac{R_s B_g}{B_o} q_o(\mathbf{r}) \bigg) |
Введем обозначение для нормированных коэффициентов межфазового обмена и их производных по давлению:
R_{vn} = \frac{B_o R_v}{B_g} |
|
R_{sn} = \frac{B_g R_s}{B_o} |
|
R_{vp} = \frac{B_o \dot R_v}{B_g} |
|
R_{sp} = \frac{B_g \dot R_s}{B_o} |
|
|
и уравнения непрерывности принимают вид: \phi s_w ( c_r + c_w ) \partial_t P_w + \phi \partial_t s_w
+ B_w \nabla \cdot \bigg ( \frac{1}{B_w} \ \mathbf{u}_w \bigg ) = q_w(\mathbf{r}) |
\phi s_o (c_r + c_o ) \partial_t P_o + \phi s_g \big( R_{vp} + R_{vn} (c_r + c_g) \big) \partial_t P_g
+ \phi \partial_t s_o + \phi R_{vn} \partial_t s_g
+ B_o \nabla \bigg ( \frac{1}{B_o} \ \mathbf{u}_o + \frac{R_{vn}}{B_o} \ \mathbf{u}_g \bigg ) = \big( q_o(\mathbf{r}) + R_{vn} q_g(\mathbf{r}) \big) |
\phi s_g ( c_r + c_g ) \partial_t P_g + \phi s_o \big( R_{sp} + R_{sn} (c_r + c_o ) \big) \partial_t P_o
+ \phi \partial_t s_g + \phi R_{sn} \partial_t s_o
+ B_g \nabla \bigg ( \frac{1}{B_g} \ \mathbf{u}_g + \frac{R_{sn}}{B_g} \ \mathbf{u}_o \bigg ) = \big( q_g(\mathbf{r}) + R_{sn} q_o(\mathbf{r}) \big) |
Введем допущение о том, что распределение объемных коэффициентов всех фаз медленно меняется по объему пласта
(что хорошо выполняется, так как объемные коэффициенты представляют собой более медленные функции, чем само давление): | \nabla B_w | \sim 0 \ , \quad | \nabla B_o | \sim 0 \ , \quad | \nabla B_g | \sim 0 |
и можно считать объемный коэффициент локально постоянным и внести его под знак градиента: \phi \big[ c_r s_w + c_w s_w \big] \partial_t P_w + \phi \partial_t s_w
+ \nabla \mathbf{u}_w = q_w |
\phi \big[ c_r s_o + c_o s_o \big] \partial_t P_o + \phi \big[ \frac{B_o}{B_g} \dot R_v s_g + \frac{B_o R_v}{B_g} (c_r s_g + c_g s_g) \big] \partial_t P_g
+ \phi \partial_t s_o + \big( \frac{\phi \ B_o \ R_v }{B_g} \big) \partial_t s_g
+ \nabla \bigg ( \mathbf{u}_o + \frac{B_o \ R_v}{B_g} \ \mathbf{u}_g \bigg ) = \bigg( q_o + \frac{R_v B_o}{B_g} q_g \bigg) |
\phi \big[ c_r s_g + c_g s_g \big] \partial_t P_g + \phi \big[ \frac{B_g}{B_o} \dot R_s s_o + \frac{B_g R_s}{B_o} (c_r s_o + c_o s_o) \big] \partial_t P_o
+ \phi \partial_t s_g + \big( \frac{\phi \ B_g \ R_s}{B_o} \big) \partial_t s_o
+ \nabla \bigg ( \mathbf{u}_g + \frac{B_g \ R_s}{B_o} \ \mathbf{u}_o \bigg ) = \bigg( q_g + \frac{R_s B_g}{B_o} q_o \bigg) |
откуда \phi \big[ c_r s_w + c_w s_w \big] \partial_t P_w + \phi \partial_t s_w
+ \nabla \mathbf{u}_w = q_w |
\phi \big[ c_r s_o + c_o s_o \big] \partial_t P_o + \phi \big[ R_{vp} s_g + R_{vn} (c_r s_g + c_g s_g) \big] \partial_t P_g
+ \phi ( \partial_t s_o + R_{vn} \partial_t s_g )
+ \nabla \bigg ( \mathbf{u}_o + R_{vn} \mathbf{u}_g \bigg ) = ( q_o + R_{vn} q_g ) |
\phi \big[ c_r s_g + c_g s_g \big] \partial_t P_g + \phi \big[ R_{sp} s_o + R_{sn} (c_r s_o + c_o s_o) \big] \partial_t P_o
+ \phi ( \partial_t s_g + R_{sn} \partial_t s_o )
+ \nabla \bigg ( \mathbf{u}_g + R_{sn} \ \mathbf{u}_o \bigg ) = ( q_g + R_{sn} q_o ) |
Подставим в вышеприведенные уравнения непрерывности выражения для скоростей каждой компоненты  –  : \phi \big[ c_r s_w + c_w s_w \big] \partial_t P_w + \phi \partial_t s_w
- \nabla \big( \alpha_w ( \nabla P_w - \rho_w \mathbf{g} ) \big) = q_w(\mathbf{r}) |
\phi \big[ c_r s_o + c_o s_o \big] \partial_t P_o + \phi \big[ R_{vp} s_g + R_{vn} (c_r s_g + c_g s_g) \big] \partial_t P_g
+ \phi ( \partial_t s_o + R_{vn} \partial_t s_g )
- \ \nabla \bigg ( \alpha _o ( \nabla P_o - \rho_o \mathbf{g}) + R_{vn} \alpha_g ( \nabla P_g -\rho_g \mathbf{g} ) \bigg ) = ( q_o + R_{vn} q_g ) |
\phi \big[ c_r s_g + c_g s_g \big] \partial_t P_g + \phi \big[ R_{sp} s_o + R_{sn} (c_r s_o + c_o s_o) \big] \partial_t P_o
+ \phi ( \partial_t s_g + R_{sn} \partial_t s_o )
- \nabla \bigg ( \alpha_g ( \nabla P_g - \rho_g \mathbf{g}) + R_{sn} \alpha_o ( \nabla P_o - \rho_o \mathbf{g} ) \bigg ) = ( q_g + R_{sn} q_o ) |
Введем понятие среднего давления по всем фазам: P = \frac{1}{3} ( P_w + P_o + P_g) |
через которое однозначно выражается давление каждой фазы:
P_w = P +\frac{1}{3} (-2 P_{cow} + P_{cog}) |
|
P_o = P +\frac{1}{3} (P_{cow} + P_{cog}) |
|
P_g = P +\frac{1}{3} (P_{cow} - 2 P_{cog}) |
|
|
и предположим, что в течение исследуемого процесса насыщенности меняются так слабо, что изменением капиллярного давления во времени и пространстве можно пренебречь: \partial_t P_{cow}(s) \sim 0 \quad \partial_t P_{cog}(s) \sim 0 \quad | \nabla P_{cow}(s) | \sim 0 \quad | \nabla P_{cog}(s) | \sim 0 |
и следовательно производные по времени и пространственные градиенты фазовых давлений определяются средне-фазовым давлением \partial_t P_w = \partial_t P_o = \partial_t P_g = \partial_t P |
\nabla P_w = \nabla P_o = \nabla P_g = \nabla P |
а уравнения непрерывности примут вид:
\phi \big[ c_r s_w + c_w s_w \big] \partial_t P + \phi \partial_t s_w
- \nabla \big( \alpha_w ( \nabla P - \rho_w \mathbf{g} ) \big) = q_w |
\phi \big[ c_r s_o + c_o s_o \big] \partial_t P + \phi \big[ R_{vp} s_g + R_{vn} (c_r s_g + c_g s_g) \big] \partial_t P
+ \phi ( \partial_t s_o + R_{vn} \partial_t s_g )
- \nabla \big( \alpha _o ( \nabla P - \rho_o \mathbf{g}) + R_{vn} \alpha_g ( \nabla P -\rho_g \mathbf{g} ) \big) = ( q_o + R_{vn} q_g ) |
\phi \big[ c_r s_g + c_g s_g \big] \partial_t P + \phi \big[ R_{sp} s_o + R_{sn} (c_r s_o + c_o s_o) \big] \partial_t P
+ \phi ( \partial_t s_g + R_{sn} \partial_t s_o )
- \nabla \big( \alpha_g (\nabla P - \rho_g \mathbf{g}) + R_{sn} \alpha_o ( \nabla P - \rho_o \mathbf{g}) \big) = ( q_g + R_{sn} q_o ) |
или \phi \big[ c_r s_w + c_w s_w \big] \partial_t P + \phi \partial_t s_w
- \nabla \big( \alpha_w \nabla P \big) + \nabla ( \alpha_w \rho_w \mathbf{g} ) = q_w |
\phi \big[ c_r s_o + c_o s_o + R_{vp} s_g + R_{vn} (c_r s_g + c_g s_g) \big] \partial_t P
+ \phi ( \partial_t s_o + R_{vn} \partial_t s_g )
- \nabla \big( (\alpha _o + R_{vn} \alpha_g) \nabla P \big) + \nabla ( \alpha_o \rho_o \mathbf{g} + R_{vn} \alpha_g \rho_g \mathbf{g} ) = ( q_o + R_{vn} q_g ) |
\phi \big[ c_r s_g + c_g s_g + R_{sp} s_o + R_{sn} (c_r s_o + c_o s_o) \big] \partial_t P
+ \phi ( \partial_t s_g + R_{sn} \partial_t s_o )
- \nabla \big( (\alpha_g + R_{sn} \alpha_o) \nabla P \big) + \nabla ( \alpha_g \rho_g \mathbf{g} + R_{sn} \alpha_o \rho_o \mathbf{g} ) = ( q_g + R_{sn} q_o ) |
В вышеприведенных уравнениях разные коэффициенты при производных зависят от фазовых давлений, например:  ,  ,  .
Но в силу слабой зависимости этих коэффициентов от давления в целом, можно пренебречь капиллярным различием в аргументах и считать, что все коэффициенты зависят от средне-фазового давления, например:  ,  ,  , хотя это конечно приводит к небольшой потере точности в расчетах.
Сложим все три уравнения и учтем, что 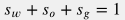 : \phi \big[ c_r (1 + R_{sn} s_o + R_{vn} s_g) + c_w s_w + c_o s_o (1+R_{sn}) + c_g s_g (1 + R_{vn}) + R_{sp} s_o + R_{vp} s_g \big] \partial_t P + \phi R_{vn} \partial_t s_g + \phi R_{sn} \partial_t s_o \, - |
- \, \nabla \big ( ( \alpha_w + \alpha_o (1+ R_{sn}) + \alpha_g (1 + R_{vn}) ) \nabla P \big )
+ \nabla (\alpha_w \rho_w \mathbf{g} + \alpha_o \rho_o \mathbf{g} + R_{vn} \alpha_g \rho_g \mathbf{g} + \alpha_g \rho_g \mathbf{g} + R_{sn} \alpha_o \rho_o \mathbf{g} )
\, = \, q_w + ( q_o + R_{vn} q_g ) + ( q_g + R_{sn} q_o ) |
Введем обозначения:
c_t = c_r (1 + R_{sn} s_o + R_{vn} s_g) + c_w s_w + c_o s_o (1+R_{sn}) + c_g s_g (1 + R_{vn}) + R_{sp} s_o + R_{vp} s_g |
|
для эффективной сжимаемости мультифазного пласта |
\alpha = \alpha_w + \alpha_o (1+ R_{sn}) + \alpha_g (1 + R_{vn}) |
|
для эффективной проводимости пласта, насыщенного мультифазным флюидом |
\rho_{\alpha} = \frac{ \alpha_{rw} \rho_w + \alpha_{ro} \rho_o (1 + R_{sn}) + \alpha_{rg} \rho_g (1+R_{vn}) }{ \alpha_{rw} + \alpha_{ro} (1 + R_{sn}) + \alpha_{rg} (1+R_{vn}) }
|
|
для эффективной плотности мультифазного флюида |
q_t = q_w + q_o + q_g = B_w \, q_W + (B_o - R_v \, B_g) \, q_O + (B_g - R_s \, B_o) \, q_G |
|
для суммарного объемного дебита источника мультифазного флюида в данной точке (пластопересечение скважины) |
и получим следующее уравнение, связывающее динамику среднефазового давления в пласте с динамикой насыщенности во времени:
\phi c_t \partial_t P + \phi R_{vn} \partial_t s_g + \phi R_{sn} \partial_t s_o - \nabla \big ( \alpha ( \nabla P - \rho_{\alpha} \mathbf{g} ) \big ) = q_t |
В предположении малости нормированных коэффициентов межфазового обмена и слабого изменения насыщенности во времени: R_{vn} \partial_t s_g \sim 0, \quad R_{sn} \partial_t s_o \sim 0 |
мы приходим к следующему уравнению мультифазной диффузии давления в пласте: \phi c_t \partial_t P - \nabla \big ( \alpha ( \nabla P - \rho_{\alpha} \mathbf{g} ) \big ) = q_t |
что внешне совпадает с уравнением однофазной фильтрации  и называется уравнением мультифазной пьезодинамики.
Напомним, что это уравнение имеет смысл только при соблюдении следующих условий: | \nabla B_w | \sim 0 \ , \quad | \nabla B_o | \sim 0 \ , \quad | \nabla B_g | \sim 0 |
R_{vn} \partial_t s_g \sim 0, \quad R_{sn} \partial_t s_o \sim 0 |
\partial_t P_{cow}(s) \sim 0 \quad \partial_t P_{cog}(s) \sim 0 |
| \nabla P_{cow}(s) | \sim 0 \quad | \nabla P_{cog}(s) | \sim 0 |
При условии незначительного изменения температуры и насыщенности в пласте за время наблюдения, условия  ,  ,  и  практически всегда выполняются в основной массе пласта, что позволяет анализировать давление мультифазного потока согласно  и получать весьма аккуратное приближение по средне-фазовому давлению к решению полной системы – .
|