Рассмотрим однофазную фильтрацию ньютоновской жидкости  : :
\phi \, c_t \, \frac{\partial p}{\partial t} + \nabla \cdot \big( \alpha \big( \nabla p - \rho {\bf g} \big) \big) + c \alpha \nabla p \cdot \big( \nabla p - \rho {\bf g} \big) = q(t, {\bf r}) |
Пласт называется слабо-сжимаемым, если: 1) параметры среды (пород и флюида), входящие в коэффициенты уравнения  не зависят от давления: не зависят от давления: 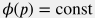 , , 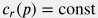 , , 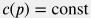 , , 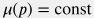 , ,  , ,
и, следовательно, 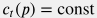 , , 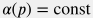
2) значение сжимаемости флюида достаточно низкое, чтобы соблюдалось условие
c \ll \frac{\Delta p}{ |\nabla p|^2 } |
в результате чего дивергентный член уравнения непрерывности  принимает вид принимает вид \nabla \cdot ( \rho {\bf u} ) = \rho \, \nabla \cdot {\bf u} + \rho \, c \, {\bf u} \cdot \nabla p = \rho \, (\nabla \cdot {\bf u} ) \bigg[ 1 + c \frac{{\bf u} \cdot \nabla p }{|\nabla {\bf u}|} \bigg] = \rho \, \nabla \cdot {\bf u} |
\frac{|\nabla {\bf u}|}{{\bf u} \cdot \nabla p } = \frac{\Delta p - {\bf g} \cdot \nabla \rho }{ |\nabla p|^2 - \rho \, {\bf g} \cdot \nabla p }= \frac{\Delta p - \rho \, c \, {\bf g} \cdot \nabla p }{ |\nabla p|^2 - \rho \, {\bf g} \cdot \nabla p }
= c \frac{(1/c) \, \Delta p - \rho \, {\bf g} \cdot \nabla p }{ |\nabla p|^2 - \rho \, {\bf g} \cdot \nabla p } \ll
c \frac{|\nabla p|^2 - \rho \, {\bf g} \cdot \nabla p }{ |\nabla p|^2 - \rho \, {\bf g} \cdot \nabla p } = c
\rightarrow |\nabla {\bf u}| \ll c {\bf u} \cdot \nabla p |
где 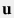 – скорость потока флюида в пласте – скорость потока флюида в пласте 
|
Отсюда получается основное уравнение однофазной диффузии в приближении слабо-сжимаемого флюида: c_t \phi \, \frac{\partial p}{\partial t} = \nabla \big( \alpha \, ( \nabla p - \rho {\bf g} ) \big) + q(t, {\bf r}) |
которое теперь является линейным дифференциальным уравнением.
Условие  по сути означает что изменение давления в объема пласте настолько медленное, что пространственным градиентом плотности можно пренебречь и следовательно по сути означает что изменение давления в объема пласте настолько медленное, что пространственным градиентом плотности можно пренебречь и следовательно \nabla p - \rho {\bf g} = \nabla ( p - \rho {\bf g}) = \nabla \tilde p |
где 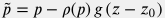 – скорректированное давление на опорную глубину – скорректированное давление на опорную глубину  (датум), которая часто выбирается на уровне ВНК. (датум), которая часто выбирается на уровне ВНК.
В результате уравнение пьезодинамики в приближении слабо-сжимаемого пласта принимает вид: c_t \phi \, \frac{\partial \tilde p}{\partial t} = \nabla \big( \alpha \, \nabla \tilde p \big) + q(t, {\bf r}) |
В случае однородного коллектора 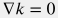 и слабой зависимости вязкости от давления и слабой зависимости вязкости от давления 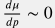 (что, как правило, всегда выполняется для слабо-сжимаемого приближения) основное уравнение пьезодинамики принимает вид: (что, как правило, всегда выполняется для слабо-сжимаемого приближения) основное уравнение пьезодинамики принимает вид: \frac{\partial \tilde p}{\partial t} = \chi \Delta \tilde p + \frac{1}{\phi c_t} q(t, {\bf r}) |
где 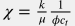 – пьезопроводность пласта (константа) и – пьезопроводность пласта (константа) и 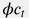 – упругоемкость пласта (константа). – упругоемкость пласта (константа).
В таблице 1 приведен явный вид уравнения однофазной пьезодинамики для наиболее популярных случаев фильтрационной симметрии.
Табл. 1
| Линейная одномерная диффузия | Радиальная одномерная диффузия | Двумерная диффузия | Трехмерная диффузия |
|---|
Неоднородный пласт
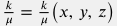
|
c_t \phi \, \frac{\partial p}{\partial t} = \frac{\partial }{\partial x} \bigg( \frac{k}{\mu} \, \frac{\partial p}{\partial x} \bigg) + q(t, x) |
|
c_t \phi \, \frac{\partial p}{\partial t} = \frac{1}{r} \frac{\partial }{\partial r} \bigg( \frac{k}{\mu} \, r \, \frac{\partial p}{\partial r} \bigg) + q(t, r) |
|
c_t \phi \, \frac{\partial p}{\partial t} = \bigg[ \frac{\partial }{\partial x} \bigg( \frac{k}{\mu} \, \frac{\partial p} {\partial x} \bigg) +
\frac{\partial }{\partial y} \bigg( \frac{k}{\mu} \, \frac{\partial p} {\partial y}\bigg)
\bigg] + q(t, x) |
|
c_t \phi \, \frac{\partial p}{\partial t} = \bigg[ \frac{\partial }{\partial x} \bigg( \frac{k}{\mu} \, \frac{\partial p} {\partial x} \bigg) +
\frac{\partial }{\partial y} \bigg( \frac{k}{\mu} \, \frac{\partial p} {\partial y} \bigg)
+
\frac{\partial }{\partial z} \bigg( \frac{k}{\mu} \, \frac{\partial p} {\partial z}\bigg)
\bigg] + q(t, x) |
| Однородный пласт
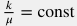
|
\frac{\partial p}{\partial t} = \chi \, \frac{\partial^2 p }{\partial x^2} + \frac{1}{\phi c_t} q(t, r) |
|
\frac{\partial p}{\partial t} = \chi \, \frac{1}{r} \frac{\partial }{\partial r} \bigg(r \, \frac{\partial p}{\partial r} \bigg) + \frac{1}{\phi c_t} q(t, r) |
|
\frac{\partial p}{\partial t} = \chi \, \bigg( \frac{\partial^2 p }{\partial x^2}
+\frac{\partial^2 p }{\partial y^2} \bigg)+ \frac{1}{\phi c_t} q(t, r) |
|
\frac{\partial p}{\partial t} = \chi \, \bigg( \frac{\partial^2 p }{\partial x^2}
+\frac{\partial^2 p }{\partial y^2}
+\frac{\partial^2 p }{\partial z^2}
\bigg)+ \frac{1}{\phi c_t} q(t, r) |
|
Список ключевых параметров однофазной фильтрационной модели
|
|
|---|
| толщина пласта, где протекает фильтрация | | пористость пласта | | фазовая проницаемость пласта для данного флюида | | вязкость флюида | | сжимаемость порового скелета | | сжимаемость флюида | | сжимаемость пласта |
|
| | проводимость пласта | | упругоемкость пласта | | гидропроводность пласта | | пьезопроводность пласта |
|