Given:
- a function
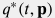of real-value argument 
and set of model parameters 
- a training data set:
the matching procedure assumes searching for thee specific set of model parameters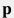 
to minimize the goal function:
F({\bf p}) = \sum_{k=1}^N \, \Psi \left( q^*(t_k) - q_k \right) \rightarrow \textrm{min} |
where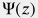 
is the discrepancy distance function.
Most popular choices are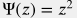 
and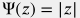 
.
There are few approaches to match the Arps decline to the historical data:
Unconstrained matching
All three model parameters 
are being varied to achieve the best fit to the training dataset.
The best-fit model may not match:
- the initial production rate
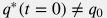
- the current production rate
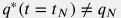
- the current cumulative production
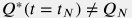
Match the value of the initial rate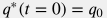 
The value of the model rate at the initial time moment is set to training dataset: 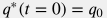and the two other model properties 
are being varied to achieve the best fit to the training dataset.
The best-fit model may not match:
- the current production rate
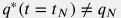
- the current cumulative production
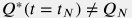
Match the value of the current rate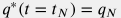 
To ensure the smooth transition from historical data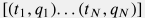 
to the production forecasts in future time moments 
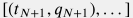one may wish to constrain the model by firm matching the production at the last historical moment 
which leads to the following form of Arp's model:
| Exponential Production Decline | Hyperbolic Production Decline | Harmonic Production Decline |
|---|
| | |
q(t)=q_N \cdot \exp \big[ -D_0 \cdot (t-t_N) \big] |
| q(t) = q_N \cdot \left[ \frac{1+b \cdot D_0 \cdot t_N }
{ 1+b \cdot D_0 \cdot t } \right]^{1/b} |
| q(t) = q_N \cdot \left[ \frac{1+D_0 \cdot t_N }
{ 1+ D_0 \cdot t } \right] |
|
Q(t) - Q_N = [ q_N - q(t)] \, \tau_0 |
| Q(t) - Q_N = \frac{q_N^b \, (\tau_0 + b \, t_N)}{1-b} \left[ q_N^{1-b} - q^{1-b}(t) \right] |
| Q(t) - Q_N = q_N \, (\tau_0 + t_N) \cdot \ln \frac{q_N}{q(t)} |
|
The best-fit model may not match:
- the initial production rate
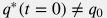
- the current cumulative production
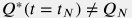
Match the value of the current cumulative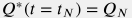 
To ensure the smooth transition from historical data 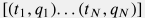to the production forecasts in future time moments 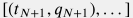one may wish to constrain the model by firm matching the production at the last historical moment which leads to the following form of Arp's model:
| Exponential Production Decline | Hyperbolic Production Decline | Harmonic Production Decline |
|---|
| | |
q(t)=q_N \cdot \exp \big[ -D_0 \cdot (t-t_N) \big] |
| q(t) = q_N \cdot \left[ \frac{1+b \cdot D_0 \cdot t_N }
{ 1+b \cdot D_0 \cdot t } \right]^{1/b} |
| q(t) = q_N \cdot \left[ \frac{1+D_0 \cdot t_N }
{ 1+ D_0 \cdot t } \right] |
|
Q(t) - Q_N = [ q_N - q(t)] \, \tau_0 |
| Q(t) - Q_N = \frac{q_N^b \, (\tau_0 + b \, t_N)}{1-b} \left[ q_N^{1-b} - q^{1-b}(t) \right] |
| Q(t) - Q_N = q_N \, (\tau_0 + t_N) \cdot \ln \frac{q_N}{q(t)} |
|
The best-fit model may not match:
- the initial production rate
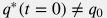
- the current production rate
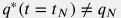
Match the value of the current rate and cumulative ,
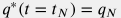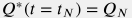
To ensure the smooth transition from historical data 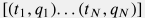to the production forecasts in future time moments 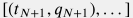one may wish to constrain the model by firm matching the production at the last historical moment which leads to the following form of Arp's model:
| Exponential Production Decline | Hyperbolic Production Decline | Harmonic Production Decline |
|---|
| | |
q(t)=q_N \cdot \exp \big[ -D_0 \cdot (t-t_N) \big] |
| q(t) = q_N \cdot \left[ \frac{1+b \cdot D_0 \cdot t_N }
{ 1+b \cdot D_0 \cdot t } \right]^{1/b} |
| q(t) = q_N \cdot \left[ \frac{1+D_0 \cdot t_N }
{ 1+ D_0 \cdot t } \right] |
|
Q(t) - Q_N = [ q_N - q(t)] \, \tau_0 |
| Q(t) - Q_N = \frac{q_N^b \, (\tau_0 + b \, t_N)}{1-b} \left[ q_N^{1-b} - q^{1-b}(t) \right] |
| Q(t) - Q_N = q_N \, (\tau_0 + t_N) \cdot \ln \frac{q_N}{q(t)} |
|
The best-fit model may not match:
- the initial production rate
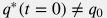
See Also
Petroleum Industry / Upstream / Production / Subsurface Production / Field Study & Modelling / Production Analysis / Decline Curve Analysis / DCA Arps @model