Definition
Mathematical model of multiphase wellbore flow predicts the temperature, pressure and flow speed distribution along the wellbore trajectory with account for:
- tubing head pressure which is set by gathering system or injection pump
- wellbore design
- pump characterisits
- fluid friction with tubing /casing walls
- interfacial phase slippage
- heat exchange between wellbore fluid and surrounding rocks
Mathematical Model
The multiphase wellbore flow in hydrodynamic and thermodynamic equilibrium is defined by the following set of 1D equations:
| LaTeX Math Block |
|---|
| anchor | MatBal |
|---|
| alignment | left |
|---|
|
\frac{\partial (\rho_m A)}{\partial t} + \frac{\partial}{\partial l} \bigg( A \, \sum_\alpha \rho_\alpha \, u_\alpha \bigg) = 0 |
| LaTeX Math Block |
|---|
|
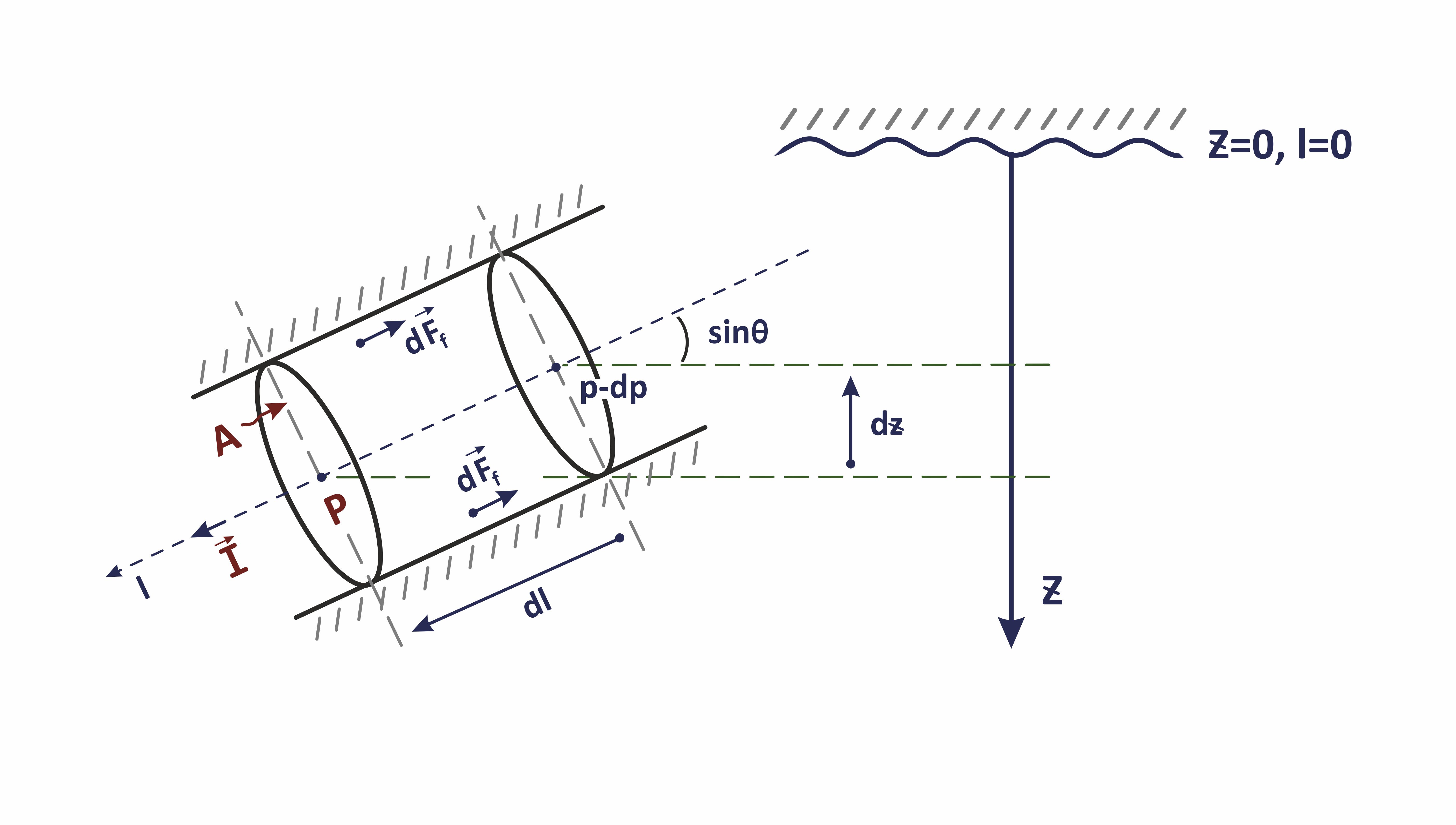
\sum_\alpha \rho_\alpha \bigg[ \frac{\partial u_\alpha}{\partial t} + u_\alpha \frac{\partial u_\alpha}{\partial l} - \nu_\alpha \Delta u_\alpha\bigg] = - \frac{dp}{dl} + \rho_m \, g \, \sin \theta - \frac{ f_m \, \rho_m \, u_m^2 \, }{2 d} |
| LaTeX Math Block |
|---|
|
(\rho \,c_p)_m \frac{\partial T}{\partial t}
- \sum_\alpha \rho_\alpha \ c_{p \alpha} \ \eta_{s \alpha} \ \frac{\partial P_\alpha}{\partial t}
+ \sum_\alpha \rho_\alpha \ c_{p \alpha} \ u_\alpha \frac{\partial T}{\partial l}
\ = \ \frac{1}{A} \ \sum_\alpha \rho_\alpha \ c_{p \alpha} T_\alpha \frac{\partial q_\alpha}{\partial l} |
where
| indicates a mixture of fluid phases |
|
| water, oil, gas phase indicator |
|
| measure length along wellbore trajectory | |
| in-situ velocity of -phase fluid flow |
| |
| cross-sectional average fluid density |
| wellbore trajectory inclination to horizon |
| cross-sectional average pipe flow diameter |
| in-situ cross-sectional area | LaTeX Math Inline |
|---|
| body | A(l) = 0.25 \, \pi \, d^2(l) |
|---|
|
|
| Darci flow friction coefficient |
| kinematic viscosity of -phase |
| temperature of -phase fluid flowing from reservoir into a wellbore |
Equations
| LaTeX Math Block Reference |
|---|
|
–
| LaTeX Math Block Reference |
|---|
|
define a closed set of 3 scalar equations on 3 unknowns: pressure
, temperature
and mixture-average fluid velocity
.
The model is set in 1D-model with
axis aligned with well trajectory
:
The disambiguation of the properties in the above equation is brought in The list of dynamic flow properties and model parameters.
Equation
| LaTeX Math Block Reference |
|---|
|
defines the continuity of the fluid components flow or equivalently represent the mass conservation of each mass component
| LaTeX Math Inline |
|---|
| body | \{ m_W, \ m_O, \ m_G \} |
|---|
|
during its transportation along wellbore.
Equation
| LaTeX Math Block Reference |
|---|
|
defines the motion dynamics of each phase (called Navier–Stokes equation), represented as linear correlation between phase flow speed
and pressure profile of mutliphase fluid
.
The term
| LaTeX Math Inline |
|---|
| body | \sum_\alpha \rho_\alpha \ c_{p \alpha} \ u_\alpha \frac{\partial T}{\partial l} |
|---|
|
represents heat convection defined by the wellbore mass flow.
The term
| LaTeX Math Inline |
|---|
| body | \sum_\alpha \rho_\alpha \ c_{p \alpha} \ \eta_{s \alpha} \ \frac{\partial P_\alpha}{\partial t} |
|---|
|
represents the heating/cooling effect of the fast adiabatic pressure change.
This usually takes effect in the wellbore during the first minutes or hours after changing the well flow regime (as a consequence of choke/pump operation).
The multiphase fluid density
is defined by exact formula:
| LaTeX Math Block |
|---|
|
\rho_m = \sum_\alpha \rho_\alpha s_\alpha |
where
– fractional volumes of
-phase which are naturally constraint by:
| LaTeX Math Block |
|---|
| anchor | s_norm |
|---|
| alignment | left |
|---|
|
\sum_\alpha s_\alpha = s_w + s_o + s_g = 1 |
The
can be also expressed as fraction of the total flowing cross-sectional area
occupied by
-phase:
| LaTeX Math Block |
|---|
| anchor | s_alpha |
|---|
| alignment | left |
|---|
|
s_\alpha = \frac{A_\alpha}{A} |
The term
defines mass-specific heat capacity of the multiphase mixture and defined by exact formula:
| LaTeX Math Block |
|---|
| anchor | rho_cp |
|---|
| alignment | left |
|---|
|
(\rho \,c_p)_m = \sum_\alpha \rho_\alpha c_\alpha s_\alpha |
The in-situ velocities
are usually expressed via the macroscopic flow velocity
using the
| Expand |
|---|
|
| LaTeX Math Block |
|---|
| (\rho \,c_{pt})_p \frac{\partial T}{\partial t}
- \sum_{a = \{w,o,g \}} \rho_\alpha \ c_{p \alpha} \ \eta_{s \alpha} \ \frac{\partial P_\alpha}{\partial t}
+ \sum_{a = \{w,o,g \}} \rho_\alpha \ c_{p \alpha} \ u_\alpha \frac{\partial T}{\partial l}
\ = \ \frac{\delta E_H}{ \delta V \delta t} |
Equation | LaTeX Math Block Reference |
|---|
|
defines the heat flow continuity or equivalently represents heat conservation due to heat conduction and convection with account for adiabatic and Joule–Thomson throttling effect.The term | LaTeX Math Inline |
|---|
| body | \frac{\delta E_H}{ \delta V \delta t} |
|---|
|
defines the speed of change of heat energy volumetric density due to the inflow from formation into the wellbore.
|
Stationary Flow Model
Stationary wellbore flow is defined as the flow with constant pressure and temperature:
| LaTeX Math Inline |
|---|
| body | \frac{\partial T}{\partial t} = 0 |
|---|
|
and
| LaTeX Math Inline |
|---|
| body | \frac{\partial P_\alpha}{\partial t} = 0 |
|---|
|
.
This happens during the long-term (usually hours & days & weeks) production/injection or long-term (usually hours & days & weeks) shut-in.
The temperature dynamic equation
| LaTeX Math Block Reference |
|---|
|
is going to be:
| LaTeX Math Block |
|---|
|
\sum_\alpha \rho_\alpha \ c_{p \alpha} \ u_\alpha \frac{\partial T}{\partial l}
\ = \ \frac{1}{A} \ \sum_\alpha \rho_\alpha \ c_{p \alpha} T_\alpha \frac{\partial q_\alpha}{\partial l} |
The phase temperature
is the temperature of the
-phase flowing from reservoir into wellbore.
It carries the original reservoir temperature with heating/cooling effect from reservoir-flow throttling and well-reservoir contact throttling:
| LaTeX Math Block |
|---|
|
T_\alpha = T_r + \epsilon_\alpha \, \delta P = T_r + \epsilon_\alpha \, (P_e - P_{wf}) |
The discrete computational scheme for
| LaTeX Math Block Reference |
|---|
|
will be:
| LaTeX Math Block |
|---|
|
\bigg( \sum_\alpha \rho_\alpha^{k-1} \ c_{p \alpha}^{k-1} \ q_\alpha^{k-1} \bigg) T^{k-1} - \bigg( \sum_\alpha \rho_\alpha^k \ c_{p \alpha}^k \ q_\alpha^k \bigg) T^k
= \sum_\alpha \rho_\alpha^k \ c_{p \alpha}^k \ (q_\alpha^{k-1} - q_\alpha^k) \, (T_r^k + \epsilon_\alpha^k \delta p^k ) |
where
| LaTeX Math Inline |
|---|
| body | \delta p^k = p_e^k - p_{wf}^k |
|---|
|
is drawdown,
– formation pressure in
-th grid layer,
– bottom-hole pressure across
-th grid layer,
– remote reservoir temperature of
-th grid layer.
The
-axis is pointing downward along hole with
-th grid layer sitting above the
-th grid layer.
If the flowrate is not vanishing during the stationary lift (
| LaTeX Math Inline |
|---|
| body | \sum_{a = \{w,o,g \}} |q_\alpha^{k-1}| > 0 |
|---|
|
) then
can be calculated iteratively from previous values of the wellbore temperature
as:
| LaTeX Math Block |
|---|
|
T^{k-1} = \frac{\bigg( \sum_\alpha \rho_\alpha^k \ c_{p \alpha}^k \ q_\alpha^k \bigg) T^k + \sum_\alpha \rho_\alpha^k \ c_{p \alpha}^k \ (q_\alpha^{k-1} - q_\alpha^k) \, (T_r^k + \epsilon_\alpha^k \delta p^k )}{\bigg( \sum_\alpha \rho_\alpha^{k-1} \ c_{p \alpha}^{k-1} \ q_\alpha^{k-1} \bigg) } |
| Expand |
|---|
|
| LaTeX Math Block |
|---|
| (\rho \,c_{pt})_p \frac{\partial T}{\partial t}
- \ \phi \sum_{a = \{w,o,g \}} \rho_\alpha \ c_{p \alpha} \ \eta_{s \alpha} \ \frac{\partial P_\alpha}{\partial t}
+ \bigg( \sum_{a = \{w,o,g \}} \rho_\alpha \ c_{p \alpha} \ \epsilon_\alpha \ \mathbf{u}_\alpha \bigg) \nabla P
+ \bigg( \sum_{a = \{w,o,g \}} \rho_\alpha \ c_{p \alpha} \ \mathbf{u}_\alpha \bigg) \ \nabla T
- \nabla (\lambda_t \nabla T) = \frac{\delta E_H}{ \delta V \delta t} |
The wellbore fluid velocity can be expressed thorugh the volumetric flow profile and tubing/casing cross-section area as:| LaTeX Math Block |
|---|
| u_\alpha = \frac{q_\alpha}{\pi r_f^2} |
so that | LaTeX Math Block |
|---|
| \bigg( \sum_{a = \{w,o,g \}} \rho_\alpha \ c_{p \alpha} \ \mathbf{u}_\alpha \bigg) \ \nabla T
= \frac{\delta E_H}{ \delta V \delta t} |
|
References
Beggs, H. D. and Brill, J. P.: "A Study of Two-Phase Flow in Inclined Pipes," J. Pet. Tech., May (1973), 607-617
| Show If |
|---|
|
| Info |
|---|
|
Физическая картина течения флюида
В зависимости от компонентного состава поток жидкости может классифицироваться как однофазный или многофазный. Первый характерен для газои водонагнетательных скважин, недавно введенных в эксплуатацию добывающих нефтяных и газовых скважин, а также сильно обводненных добывающих скважин, в то время как второй тип встречается, как правило, в большинстве скважин, находящихся в эксплуатации в течение длительного времени. В общем случае, анализ многофазного потока может быть произведен для четырехфазного потока, включающего следующие фазы: - Пластовая вода;
- Нагнетаемая вода;
ФИЗИЧЕСКИЕ ОСНОВЫ ТЕЧЕНИЯ ФЛЮИДА
Для определения расхода потока жидкости или газа, или многофазного потока необходимо знать среднюю линейную скорость смеси. Причем общий расход жидкости Q соотносится со средней линейной скоростью потока (v ̅) следующим образом:
Q=v̅A, (1.1)
где Q – дебит скважины (м3/сут), а А – площадь поперечного сечения, рассчитываемого по внутреннему диаметру обсадной колонны/ствола скважины (м2).
По данным механической расходометрии или термоиндикатора притока определяется кажущаяся линейная скорость потока vAPP. Средняя скорость потока прямо пропорциональна кажущейся скорости потока:
v̅=kVPCF•vAPP, (1.2)
где kVPCF – поправочный коэффициент для профиля скорости, зависящего от режима потока в стволе и конфигурации механического расходомера, и определяемого как функция числа Рейнольдса (Re) и отношения радиуса лопастей вертушки (r) к внутреннему радиусу ствола (R) [2]:
kVPCF=f(Re, ), (1.3)r
— R
В механике жидкостей число Рейнольдса Re является безразмерной величиной, определяющей отношение инерционных сил к силам вязкости при заданном режиме потока [2]:
- Турбулентный поток реализуется при высоких значениях числа Рейнольдса, при этом преобладают инерционные силы, что приводит к образованию хаотических завихрений и прочих нестабильностей потока. Значение числа Рейнольдса, как правило, выше 2300.
ИЗМЕРЕНИЕ МНОГОФАЗНОГО ПОТОКА
Датчики расхода и датчики состава, включенные в связку приборов Indigo PLT, измеряют средние характеристики по поперечному сечению прибора, которые зависят от режима течения многофазной смеси.
В многофазном потоке типичные режимы течения можно выделить по соотношению между приведенными скоростями фаз.
Режимы газо-жидкостного потока в вертикальных и горизонтальных трубах показаны, соответственно, на рис. 1.16 и 1.17.
Для вертикальных потоков общепринятым является выделение пузырькового (bubble), снарядного (slug), эмульсионного (churn),
Re==, (1.4)inertial forces ρvd
где
———————— ——
viscous forcesμ
дисперсно-кольцевого (annular with droplets)
и кольцевого (annular) режима течения (рис. 1.16). В случаях, когда приведенная скорость
ρ – плотность смеси
v – скорость потока
d – внутренний диаметр колонны
μ – динамическая вязкость
Число Рейнольдса зависит от скорости потока и является важным параметром, показывающим, является ли поток ламинарным или турбулентным [2]:
- Ламинарный поток имеет место при низких значениях числа Рейнольдса, при которых вязкие силы являются преобладающими, и характеризуется плавным и стабильным движением жидкости. Значение числа Рейнольдса, как правило, не превышает 2300.
газовой фазы мала, пузырьковый режим течения является преобладающим. По мере возрастания приведенной скорости газовой фазы проявляется тенденция к слиянию пузырьков с образованием «пузырьков Тейлора», при этом пузырьковый режим сменяется снарядным. При дальнейшем увеличении скорости газовой фазы снарядный режим переходит в эмульсионный режим и далее в кольцевой, при котором газ движется в ядре потока, а вся жидкость движется по стенке трубы. При кольцевом режиме течения и относительно небольших скоростях газа, часть жидкости в виде капелек может двигаться в газовом ядре потока [3].
Для горизонтальных потоков принято выделять кольцевой (annular) дисперсионно-пузырьковый (dispersed bubble), снарядный (slug), пузырьковый с горизонтально-удлиненными пузырьками (elongated bubble flow), расслоенно-волновой (stratified wavy) и расслоенный (stratified) режимы течения (рис. 1.17). Особенностью течения в горизонтальных и наклонных трубах является асимметрия в распределении фаз по сечению канала за счет действия силы тяжести [3].
В многофазном потоке каждая фаза имеет собственную относительную скорость. Разница между скоростями фаз зависит от физических свойств каждой фазы, угла наклона ствола скважины и режима течения. Разница скоростей каждой дисперсной фазы относительно непрерывной фазы называется скоростью проскальзывания v21:
v21=v2̅ v1̅ , (1.5)
где v1 – скорость непрерывной фазы, а v2 – скорость дисперсной фазы. Благодаря эффекту проскальзывания истинная насыщенность фаз не соответствует расходной насыщенности. Истинная насыщенность фазы в поперечном сечении определяется как доля, занимаемая той или иной фазой в поперечном сечении ствола скважины [4,5]:
αi=—. (1.6)Ai A
Существует ряд корреляций – эмпирических, основанных на экспериментальных данных, и механистических, основанных на принципах механики жидкостей, – для определения режимов течения и скорости проскальзывания v21. Краткое описание наиболее распространенных корреляций и областей их применения приведено в Таблицах 1.1 и 1.3.
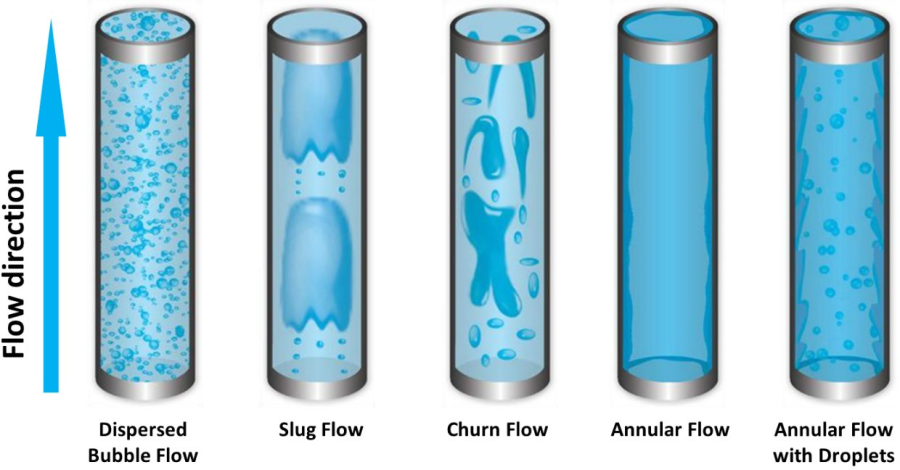
Рис. 1.16. Режимы течения многофазного потока «газ-жидкость» в вертикальной трубе [4,5].
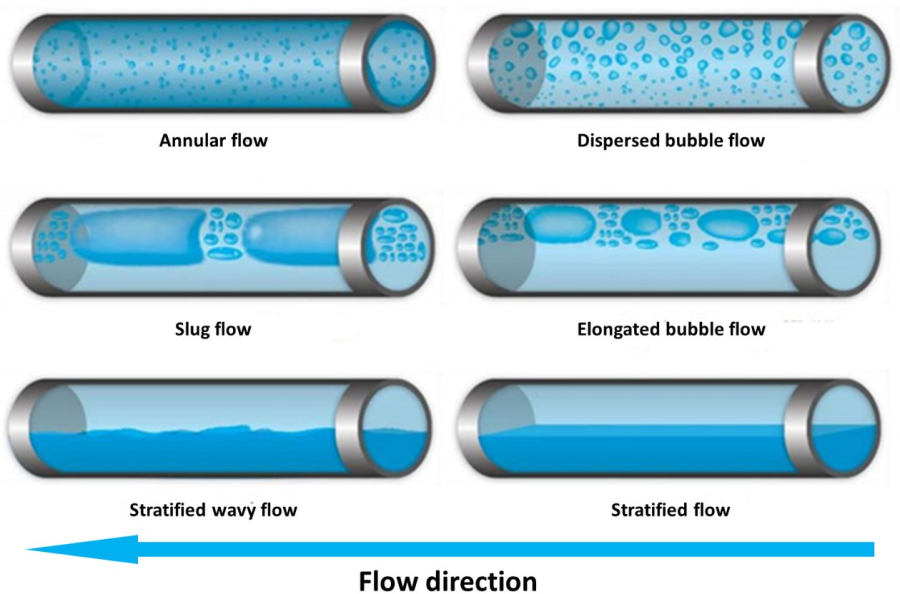
Рис. 1.17. Режимы течения многофазного потока «газ-жидкость» в горизонтальной трубе [4,5].
Таблица 1.1. Описание корреляций «жидкость-газ» («нефть-газ» или «вода-газ»)
Модель
| Модель
Тип скважины по углу наклона | Режимы многофазного потока |
Примечания
|
Ансари [6]
| Вертикальная или с незначительным углом |
Пузырьковый, снарядный, дисперсный
|
Механистическая модель
|
Бегз и Брилл [7]
| Горизонтальная или сильно наклонная (с большим зенитным углом) |
Расслоенный, прерывистый (снарядный), дисперсный (пузырьковый)
|
Эмпирическая модель
|
Стенфордская модель скорости дрейфа трехфазной смеси
(газ-жидкость) [8,9]
|
0–88°
|
От пузырькового до кольцевого
| Полумеханистическая модель, основанная на теории скорости дрейфа, с использованием эмпирически определенных параметров и соблюдением условия непрерывности между различными режимами течения. Применяется при объемных содержаниях газа свыше 0.06. |
Таблица 1.2. Описание корреляций «жидкость-жидкость» («нефть-вода»).
Модель
|
Тип скважины по углу наклона
|
Режимы многофазного потока
|
Примечания
|
Шокетт
|
Вертикальная или с незначительным углом
|
Пузырьковый
| Эмпирическая модель, в которой скорость проскальзывания фаз определяется с использованием семейства кривых, представляющих зависимость скорости проскальзывания от разницы плотности фаз и удельного содержания тяжелой фазы α_w (влагосодержание). Данная модель не учитывает различия между гидрофильными (капельки нефти в воде) и гидрофобными (капельки воды в нефти) смесями. |
Николас и Виттерхольт [10]
|
Вертикальная или наклонная (с зенитным углом до 70о)
|
Пузырьковый, псевдоснарядный
| Полуэмпирическая модель, основанная на данных экспериментального исследования и допущениях модели скорости дрейфа. Данная модель не учитывает различия между гидрофильными (капельки нефти в воде)
и гидрофобными (капельки воды в нефти) смесями. | Стенфордская модель скорости дрейфа («жидкость-жидкость»)
[4,5] |
0–88°
|
Пузырьковый, псевдоснарядный
|
Полумеханистическая модель, основанная на теории скорости дрейфа, с использованием эмпирически определенных параметров.
|
Таблица 1.3. Описание корреляций трехфазной смеси («газ-нефть-вода»).
Модель
| Тип скважины по углу наклона | Режимы многофазного потока |
Примечания
|
Стенфордская модель скорости дрейфа трехфазной смеси
[8,9]
|
0–88°
|
От пузырькового до кольцевого
| Полумеханистическая модель, основанная на теории скорости дрейфа, с использованием эмпирически определенных параметров и соблюдением условия непрерывности между различными режимами течения. Применяется при объемных содержаниях газа свыше 0,06. |
Дебиты фаз
| Section |
|---|
| Column |
|---|
| | LaTeX Math Block |
|---|
| Q_w = \sigma_{bh} \ \xi_w \ u_w |
| LaTeX Math Block |
|---|
| Q_o = \sigma_{bh} \ \xi_o \ u_o |
| LaTeX Math Block |
|---|
| Q_g = \sigma_{bh} \ \xi_g \ u_g |
|
| Column |
|---|
| | LaTeX Math Block |
|---|
| u_w = \sigma_{bh} \ \frac{\xi_w}{\mu_w} \frac{d P_{\delta}}{dh} |
| LaTeX Math Block |
|---|
| u_o = \sigma_{bh} \ \frac{\xi_o}{\mu_o} \frac{d P_{\delta}}{dh} |
| LaTeX Math Block |
|---|
| u_g = \sigma_{bh} \ \frac{\xi_g}{\mu_g} \frac{d P_{\delta}}{dh} |
|
|
Распределение давления
| LaTeX Math Block |
|---|
| Q(h) = Q_w + Q_o + Q_g = \int_{\Gamma_h} \big( q_w(h) + q_o(h) + q_g(h) \big) \ dh |
| LaTeX Math Block |
|---|
| Q(h) = \sigma_{bh}^2 \bigg( \frac{\xi_w^2}{\mu_w} + \frac{\xi_o^2}{\mu_o} + \frac{\xi_g^2}{\mu_g} \bigg)\frac{d P_{\delta}}{dh} |
откуда | LaTeX Math Block |
|---|
| P_{\delta}(t, \delta h) = \int_0^{\delta h} \frac{Q(h) \ dh}{\sigma_{bh}^2 \bigg( \frac{\xi_w^2}{\mu_w} + \frac{\xi_o^2}{\mu_o} + \frac{\xi_g^2}{\mu_g} \bigg)} |
|
|
The list of dynamic flow properties and model parameters
| time and space corrdinates , -axis is orientated towards the Earth centre, define transversal plane to the -axis |
| LaTeX Math Inline |
|---|
| body | \mathbf{r} = (x, \ y, \ z) |
|---|
|
| position vector at which the flow equations are set |
| measured depth along borehole trajectory | LaTeX Math Inline |
|---|
| body | dl^2 = dx^2 + dy^2 + dz^2 |
|---|
|
starting from tubing head | LaTeX Math Inline |
|---|
| body | l (x = x_0, \ y=y_0, \ z = z_{THP}) = 0 |
|---|
|
|
| LaTeX Math Inline |
|---|
| body | q_{mW} = \frac{d m_W}{dt} |
|---|
|
| speed of water-component mass change in wellbore draining points |
| LaTeX Math Inline |
|---|
| body | q_{mO} = \frac{d m_O}{dt} |
|---|
|
| speed of oil-component mass change in wellbore draining points |
| LaTeX Math Inline |
|---|
| body | q_{mG} = \frac{d m_G}{dt} |
|---|
|
| speed of gas-component mass change in wellbore draining points |
| LaTeX Math Inline |
|---|
| body | q_W = \frac{1}{\rho_W^{\LARGE \circ}} \frac{d m_W}{dt} = \frac{d V_{Ww}^{\LARGE \circ}}{dt} = \frac{1}{B_w} q_w |
|---|
|
| volumetric water-component flow rate in wellbore draining points recalculated to standard surface conditions
|
| LaTeX Math Inline |
|---|
| body | q_O = \frac{1}{\rho_O^{\LARGE \circ}} \frac{d m_O}{dt} = \frac{d V_{Oo}^{\LARGE \circ}}{dt} + \frac{d V_{Og}^{\LARGE \circ}}{dt} = \frac{1}{B_o} q_o + \frac{R_v}{B_g} q_g |
|---|
|
| volumetric oil-component flow rate in wellbore draining points recalculated to standard surface conditions
|
| LaTeX Math Inline |
|---|
| body | q_G = \frac{1}{\rho_G^{\LARGE \circ}} \frac{d m_G}{dt} = \frac{d V_{Gg}^{\LARGE \circ}}{dt} + \frac{d V_{Go}^{\LARGE \circ}}{dt} = \frac{1}{B_g} q_g + \frac{R_s}{B_o} q_o |
|---|
|
| volumetric gas-component flow rate in wellbore draining points recalculated to standard surface conditions
|
| LaTeX Math Inline |
|---|
| body | q_w = \frac{d V_w}{dt} |
|---|
|
| volumetric water-phase flow rate in wellbore draining points
|
| LaTeX Math Inline |
|---|
| body | q_o = \frac{d V_o}{dt} |
|---|
|
| volumetric oil-phase flow rate in wellbore draining points
|
| LaTeX Math Inline |
|---|
| body | q_g = \frac{d V_g}{dt} |
|---|
|
| volumetric gas-phase flow rate in wellbore draining points
|
| LaTeX Math Inline |
|---|
| body | q^S_W =\frac{dV_{Ww}^S}{dt} |
|---|
|
| total well volumetric water-component flow rate |
| LaTeX Math Inline |
|---|
| body | q^S_O = \frac{d (V_{Oo}^S + V_{Og}^S )}{dt} |
|---|
|
| total well volumetric oil-component flow rate
|
| LaTeX Math Inline |
|---|
| body | q^S_G = \frac{d (V_{Gg}^S + V_{Go}^S )}{dt} |
|---|
|
| total well volumetric gas-component flow rate
|
| LaTeX Math Inline |
|---|
| body | q^S_L = q^S_W + q^S_O |
|---|
|
| total well volumetric liquid-component flow rate
|
| LaTeX Math Inline |
|---|
| body | \vec u_w = \vec u_w (t, \vec r) |
|---|
|
| water-phase flow speed distribution and dynamics
|
| LaTeX Math Inline |
|---|
| body | \vec u_o = \vec u_o (t, \vec r) |
|---|
|
| oil-phase flow speed distribution and dynamics
|
| LaTeX Math Inline |
|---|
| body | \vec u_g = \vec u_g (t, \vec r) |
|---|
|
| gas-phase flow speed distribution and dynamics
|
| LaTeX Math Inline |
|---|
| body | \vec g = (0, \ 0, \ g) |
|---|
|
| gravitational acceleration vector |
| gravitational acceleration constant
|
| mass density of -phase fluid |
| viscosity of -phase fluid |
| LaTeX Math Inline |
|---|
| body | \lambda_t(P,T,s_w, s_o, s_g) |
|---|
|
| effective thermal conductivity of the rocks with account for multiphase fluid saturation |
| rock matrix thermal conductivity |
| thermal conductivity of -phase fluid |
| rock matrix mass density |
| differential adiabatic coefficient of -phase fluid |
| specific isobaric heat capacity of the rock matrix |
| specific isobaric heat capacity of -phase fluid |
| LaTeX Math Inline |
|---|
| body | \epsilon_\alpha (P, T) |
|---|
|
| differential Joule–Thomson coefficient of -phase fluid дифференциальный коэффициент Джоуля-Томсона фазы |