@wikipedia

For sample sets of two statistical variables $\begin{array}{l}x=\{x_i \, | \, i=1..n \}\end{array}$ and $\begin{array}{l}y=\{y_i \, | \, i=1..n \}\end{array}$ :

(1)	$\begin{array}{l}\displaystyle \rho_P(x,y) = \frac{{\rm cov}(x,y)}{\sigma(x) \sigma(y)} = \frac{ \sum\limits^n_{i=1} (x_i - \bar x)( y_i - \bar y)}{\sqrt{\sum\limits_i (x_i - \bar x)^2} \cdot \sqrt{\sum\limits_i (y_i - \bar y)^2}}\end{array}$

where

$\begin{array}{l}\displaystyle \bar x = \frac{1}{n} \sum\limits_{i=1}^n x_i\end{array}$	sample mean of variable $\begin{array}{l}x\end{array}$
$\begin{array}{l}\displaystyle \bar y = \frac{1}{n} \sum\limits_{i=1}^n y_i\end{array}$	sample mean of variable $\begin{array}{l}y\end{array}$

$\begin{array}{l}x=\{ x_1, \, x_2, \, ... x_n \}\end{array}$ and $\begin{array}{l}y=\{ y_1, \, y_2, \, ... y_n \}\end{array}$	finite arrays of $\begin{array}{l}x\end{array}$ -variable and $\begin{array}{l}y\end{array}$ -variable values
$\begin{array}{l}{\rm cov}(x,y)\end{array}$	covariance between $\begin{array}{l}x\end{array}$ -variable and $\begin{array}{l}y\end{array}$ -variable
$\begin{array}{l}\sigma(x)\end{array}$ , $\begin{array}{l}\sigma(y)\end{array}$	standard deviation of $\begin{array}{l}x\end{array}$ -variable and $\begin{array}{l}y\end{array}$ -variable

Pearson correlation coefficient ranges between -1 and 1 and indicates how accurately the two variables can be approximated by a linear correlation:

$\begin{array}{l}\displaystyle y_i = a \, x_i + b, \quad \forall \, i=1..n\end{array}$

with a certain pick on $\begin{array}{l}a\end{array}$ and $\begin{array}{l}b\end{array}$ .

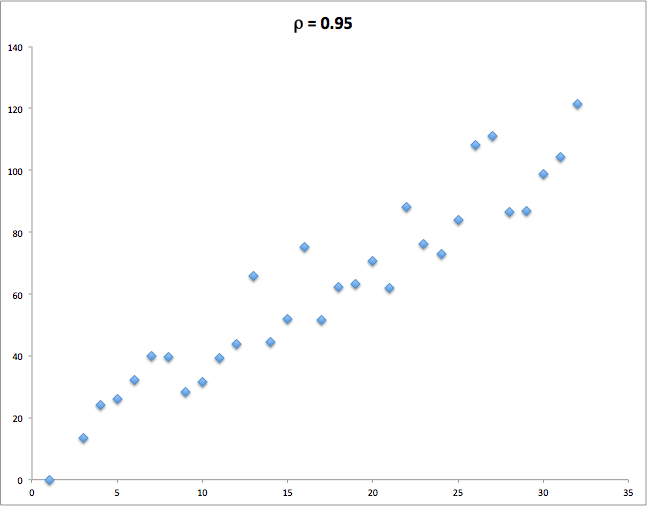
Maximum value $\begin{array}{l}\rho_p(x,y) = + 1\end{array}$ relates to perfect linear correlation with $\begin{array}{l}a>0\end{array}$ (see also Fig. 1)
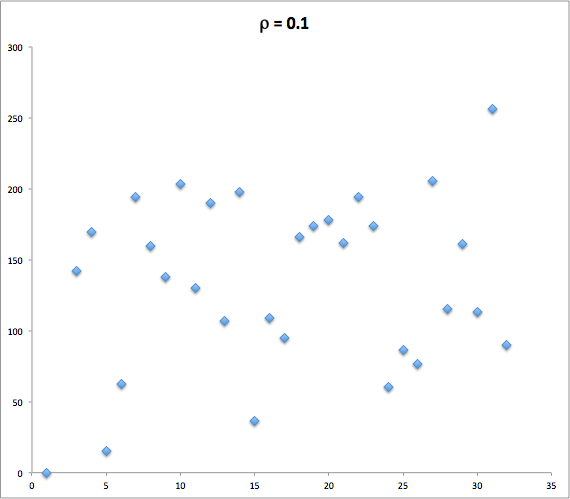
Zero value $\begin{array}{l}\rho_p(x,y) = 0\end{array}$ relates to absence of correlation between $\begin{array}{l}x\end{array}$ and $\begin{array}{l}y\end{array}$ (see also Fig. 2)
Minimum value $\begin{array}{l}\rho_p(x,y) = - 1\end{array}$ relates to perfect linear correlation with $\begin{array}{l}a< 0\end{array}$ (also called anti-correlation) (see also Fig. 3)


Fig. 1. Highly correlated variables	Fig. 2. Poorly correlated variables	Fig. 3. Highly anti-correlated variables

Page tree

See also